Определение порождающего многочлена кода БЧХ

Методические указания.

Обработка экспериментальных данных.

3.1. Сопоставив величины 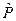и 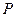, убедиться в корректности выполненного вычислительного эксперимента.

3.2. Исходные данные и результаты расчётов представить в виде таблицы 1.1, которую рекомендуется оформить в следующем виде.

Таблица 1.1.

Вероятность ошибки в канале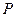
Заданные параметры кода Рез-ты вычислений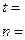
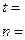
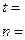
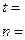
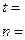
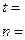
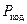
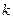
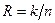
Оценка вероятности ошибки в канале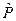

3.3. Проанализировав данные, представленные в табл.1.1, сделать выводы о влиянии на вероятность ошибки в системе с кодеком исправляющей способности и скорости кода.

3.4. Оформить отчёт о лабораторной работе

Как известно [1], примитивным кодом БЧХ, исправляющим 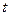ошибок, называется код длиной над полем , для которого элементы являются корнями порождающего многочлена . (Здесь 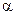− примитивный элемент расширения поля ). При этом порождающий многочлен определяется из выражения

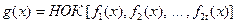, (1)

где 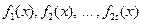− минимальные многочлены корней соответственно . Как показано в [2], минимальный многочлен для любой чётной степени 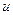элемента 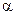совпадает с одним из минимальных многочленов нечётной степени 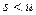этого элемента, поэтому в выражении (1) при вычислении НОК имеет смысл использовать только , соответствующие нечётным значениям 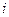. На практике для определения порождающего многочлена пользуются специальной таблицей минимальных многочленов (см. таблицу П.2 приложения) и выражением для порождающего многочлена, имеющим вид:

. (2)

При этом поступают следующим образом. По заданной длине кода 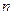и кратности исправляемых ошибок 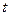определяют:

− из выражения − значение параметра , который является максимальной степенью сомножителей ;

− из выражения − максимальный порядок минимального многочлена, входящего в число сомножителей .

После этого из колонки таблицы П.2, соответствующей найденному значению выбираются коды многочленов с порядками от 1 до , записанные в восьмеричной системе счисления. Далее восьмеричные коды переводятся в двоичные, которые затем представляются в виде многочленов над полем 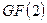. Результатом перемножения этих многочленов, выполняемого по правилам поля 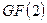, в соответствии с выражением (2) и является искомый порождающей многочлен . При выполнении лабораторной работы необходимые вычисления целесообразно выполнить с использованием возможностей программного пакета Matlab в интерактивном режиме.

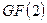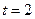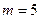Для иллюстрации изложенного рассмотрим следующий пример. Определим значение порождающего многочлена для построения примитивного кода БЧХ над длины 31, обеспечивающего . При этом имеем: Из таблицы минимальных многочленов при и получаем: 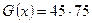. После преобразования восьмеричных кодов в двоичные имеем: и . Далее целесообразно продолжить решение задачи с использованием возможностей пакета Matlab. При этом полиномы над полем 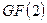соответствующие найденным кодам в командном окне системы Matlab задаются как [3]

; .

Умножение полиномов осуществляется с помощью команды , и записывается в виде: . В результате выполнения данной команды получаем код , который соответствует полиному .

В том случае, если для определения нужно перемножить не два, а более многочленов, результат также можно получить с помощью команды путём последовательного попарного умножения отдельных компонент результирующего произведения (например, если , то сначала вычисляется , а затем − ).

4.2. Кодирование (формирование разрешённой комбинации кода).

Кодирование, т.е. формирование кодовых слов 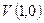систематического кода БЧХ (также как и любого другого систематического циклического кода) заключается в преобразовании информационной последовательности, представленной в виде полинома , в соответствии с выражением

, (3)

где − количество проверочных разрядов кода , а 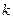−число информационных разрядов этого кода.

При этом многочлен 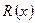, задающий проверочные разряды кода, определяется из соотношения:

(4)

(т.е 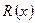есть остаток (вычет ) от деления полинома на ).

Рассмотрим пример реализации данной процедуры в системе Matlab. Закодируем информационную комбинацию кодом БЧХ (31,21), исправляющим ошибки кратностью не более 2 . Образующий многочлен этого кода был определён выше.

Полином над полем 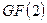, соответствующий слагаемому в сумме (3), для рассматриваемой информационной комбинации 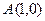в командном окне системы Matlab задаётся как

При записи этой команды был учтён тот факт, что умножение многочлена на эквивалентно добавлению справа нулей к соответствующей кодовой комбинации .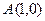

Для определения задаваемого выражением (4) остатка 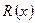следует воспользоваться командой 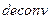, записав:

.

Первый элемент возвращаемого этой командой вектора представляет частное от деления , а второй − −остаток, который и определяет проверочные разряды кода. Результаты выполнения этой команды в рассматриваемом примере выглядят так:

;

;

Искомая кодовая комбинация 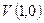может быть определена с использованием команды . Получаемый при этом результат имеет вид:

.

Дата добавления: 2015-07-02