Декодирование принимаемой кодовой комбинации

Предположим, что при прохождении по каналу связи сформированная в п.4.2 комбинация 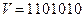вследствие воздействия помех превратилась в принимаемую кодовую комбинацию 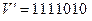, т.е. произошла одна ошибка в 3-м слева разряде. (Отметим, что в реальной ситуации, моделируемой в лабораторной работе, переданная комбинация 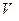и местонахождение ошибки неизвестны.)

Процесс определения ошибки и её исправления начинается с вычисления синдрома принятой кодовой комбинации. Как известно [2], вектор элементов синдрома 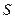может быть определён путём перемножения (с использованием правил выполнения арифметических операций в поле 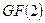) вектора принятого блока кода 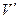на транспонированную проверочную матрицу , т.е. 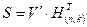. Подставляя в это равенство рассматриваемые в нашем примере значение 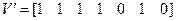и задаваемую выражением (6) матрицу и производя необходимые вычисления, получаем:

.

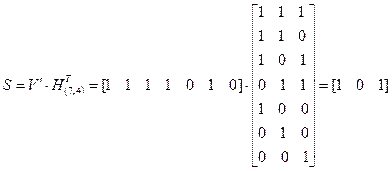Сравнивая найденный синдром со столбцами матрицы , можно убедиться, что он совпадает с третьим слева столбцом. Это и говорит о наличии ошибки в третьем слева разряде. Поскольку рассматриваемый код является двоичным, для исправления ошибки достаточно изменить значение третьего справа разряда принятого блока кода на противоположное.

В командном окне пакета Matlab процедуру определения синдрома можно реализовать следующим образом:

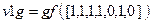; % задаём в поле 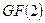вектор , %соответствующий принятой кодовой комбинации

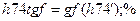задаём транспонированную матрицу (она %была введена ранее при выполнении п.4.1) в поле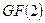

;% вычисляем вектор синдрома в поле

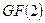
;% переводим вычисленный в поле 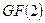вектор %синдрома в поле действительных чисел

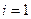; % инициализируем переменную , которая далее укажет номер разряда с ошибкой

% создаём цикл поиска разряда с ошибкой

;

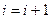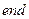
% выводим на экран номер разряда с ошибкой

4.4. Краткое описание алгоритма моделирующей программы и методики работы с ней.

Блок-схема укрупненного алгоритма моделирующей программы представлена на рис.1.1. она включает в себя 5 блоков. В блоке 1 осуществляется ввод определяющих режим моделирования данных. К их числу относятся: значение вероятности ошибки 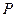в дискретном канале, а также исправляющая способность исследуемого кода и длина кодовой комбинации 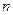. В блоке 2 по заданным 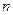и определяется количество информационных разрядов в кодовой комбинации исследуемого кода, а также производится формирование последовательности передаваемых равновероятных двоичных сообщений (символов), разбиение её на блоки, содержащие по символов, и кодирование их исследуемым кодом. Посредством блоков 3, 4 и 5 осуществляется моделирование дискретного симметричного канала без памяти, включающего в себя передатчик (блок 3) и приёмник (блок 5) модема с фазоманипулированным (ФМ) сигналом и непрерывный канал (блок 4), имитирующий линию связи. В блоке 3 закодированная последовательность двоичных символов преобразуется в отсчёты соответствующего ей фазоманипулированного (ФМ) сигнала, передаваемого в канал связи. В качестве модели непрерывного канала в данной работе используется гауссов канал (т.е. канал с аддитивным гауссовским шумом). При этом соотношение «сигнал-шум» в непрерывном канал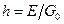е , где − энергия одной посылки сигнала; 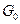− односторонний энергетический спектр шума, выбирается из условия обеспечения заданной вероятности ошибки 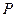в дискретном симметричном канале с ФМ, образуемом блоками 3, 4 и 5 рассматриваемой модели, на основе известного соотношения: 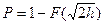, где 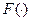− интеграл вероятностей. В блоке 4 осуществляется измерение энергии модулированного сигнала, соответствующего передаче одного элементарного сообщения, а затем формируются отсчеты дискретного белого гауссовского шума, энергетический спектр которого при измеренном значении обеспечивает заданное на моделирование отношение «сигнал-шум» 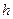. Отсчеты этого шума складываются с отсчетами передаваемого сигнала, формируя тем самым выходной сигнал непрерывного канала.

В блоке 5 производится моделирование оптимального приемника ФМ сигнала, осуществляющего его демодуляцию. Полученные при этом оценки принимаемых символов сравниваются с символами, сформированными на выходе блока 2; при несовпадении фиксируются ошибки. Отношение количества обнаруженных ошибок к общему числу переданных символов кода и представляет собой оценку вероятности ошибки в дискретном канале.

В блоке 6 полученная после демодуляции последовательность кодовых символов декодируется. Результат декодирования сравнивается с сформированной в блоке 2 последовательностью передаваемых равновероятных двоичных сообщений (подлежащей дальнейшему кодированию), при несовпадении символов фиксируются ошибки. Отношение числа ошибок к общему количеству передаваемых двоичных сообщений (которое меньше числа переданных символов кода, поскольку включает только информационные символы передаваемых кодовых комбинаций) и представляет собой оценку вероятности ошибки в системе с кодеком.

Для запуска моделирующей программы необходимо в командном окне системы Matlab набрать название программы lab_rab_1,2 и нажать клавишу Enter. Также программу можно запустить щелчком левой кнопки мыши по кнопке Run (зелёный треугольник) на панели инструментов окна Editor системы Matlab (при условии, что в этом окне активирована программа lab_rab_1,2). После запуска программы в командном окне появляется сообщение: “Введите значение вероятности ошибки в канале без кодека p=”. При его получении нужно ввести (т.е. набрать в командном окне) значение 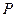в соответствии с вариантом задания и нажать клавишу Enter. При этом в качестве символа, разделяющего целую и дробную части числа при его десятичном представлении следует использовать не запятую, а точку. Получив два последующих сообщения “Введите значение исправляющей спосбности t =” и “Введите длину кодовой комбинации кода n =”нужно аналогичным образом ввести запрашиваемые программой данные. Поскольку коды Хемминга способны исправлять только одиночные ошибки, при выполнении данной лабораторной работы всегда следует вводить 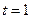. После этого начинается выполнение программы. Этапы её выполнения индицируются сообщениями, выводимыми на экран (в командном окне). По окончании выполнения программы в командном окне выводятся значения , (p_kan) и (p_kod), являющиеся результатами компьютерного эксперимента.

Контрольные вопросы

1. Изложите методику определения параметров и кода Хемминга по заданной длине кодовой комбинации .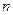

2. Изложите методику построения проверочной матрицы кода Хемминга.

3. Изложите методику построения образующей матрицы кода Хемминга.

4. Как осуществляется кодирование кодом Хемминга?

5. Что такое синдром?

6. Изложите методику определения синдрома.

7. Как осуществляется кодирование кодом Хемминга в пакете Matlab?.

8. Как осуществляется определение синдрома в пакете Matlab?.

9. Как определяется местонахождение ошибки в принятой кодовой комбинации и как она исправляется?

10. Как осуществляется определение местонахождение ошибки в принятой кодовой комбинации с использованием пакета Matlab?

12. Какими параметрами задаётся код Хемминга?

13. Как построена моделирующая программа (привести ее алгоритм)?

14. Как оценивается вероятность ошибки в дискретном канале (без кодека)?

15. Как оценивается вероятность ошибки в системе с кодеком?

16. Как зависит вероятность ошибки в системе с кодеком от скорости кода?

Литература

1.Конспект лекций.

2. Блейхут Р. Теория и практика кодов, контролирующих ошибки.− М. «Мир», 1986 г.

Приложение

Таблица П.1. Варианты заданий к лабораторной работе № 1

№ вар.		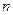Кодируемая последовательность	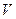Принятая последовательность	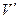Вероятность ошибки в канале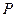
				0.01
				0.015
				0.025
				0.05
				0.07
				0.095
				0.048
				0.033
				0.084
				0.056
				0.027
				0.039
				0.013
				0.072
				0.087
				0.065
				0.019
				0.063
				0.1
				0.077
				0.042
				0.029
				0.069
				0.054
				0.092
				0.035
				0.021
				0.058
				0.017
				0.044
				0.075
				0.099
				0.019
				0.038
				0.066
				0.088
				0.097
				0.012
				0.031
				0.068
				0.093
				0.016
				0.034
				0.055
				0.081
				0.096
				0.064
				0.018
				0.036
				0.094

Дата добавления: 2015-07-02