Формирование проверочной и образующей матриц кода Хемминга

Методические указания.

Обработка экспериментальных данных.

3.1. Сопоставив величины и 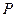, убедиться в корректности выполненного вычислительного эксперимента.

3.2. Исходные данные и результаты расчётов представить в виде таблицы 1.1, которую рекомендуется оформить в следующем виде.

Таблица 1.1.

Вероятность ошибки в канале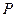
Заданные параметры кода Рез-ты вычислений
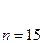
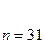
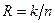
Оценка вероятности ошибки в канале

3.3. Проанализировав данные, представленные в табл.1.1, сделать выводы о влиянии на вероятность ошибки в системе с кодеком скорости кода.

3.4. Оформить отчёт о лабораторной работе

Как известно [1], параметры кода Хемминга удовлетворяют следующему соотношению:

,

где 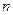− общее число разрядов в блоке кода; − число информационных разрядов; 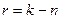− число проверочных разрядов. Поэтому при заданном значении величины и могут быть определены как

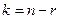; . (1)

Проверочная матрица кода Хемминга имеет размерность 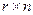и в канонической форме может быть представлена в виде:

, (2)

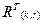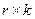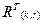где − единичная матрица размером ; - прямоугольная матрица размером , столбцами которой являются все возможные разные –разрядные комбинации двоичного кода, не совпадающие с кодовыми словами, имеющими место в столбцах матрицы (символ в обозначении означает транспонирование).

Транспонируя полученную таким образом матрицу 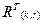, можно получить матрицу , а по ней построить порождающую матрицу

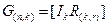, (3)

имеющую размерность .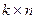

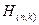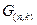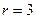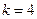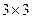Рассмотрим пример построения матриц и для кода Хемминга с . Воспользовавшись соотношениями (2), определяем, что в этом случае и . При этом единичная матрица имеет размер и выглядит так:

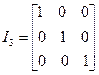. (4)

Матрицу 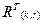размерностью получим, записывая в качестве четырёх её столбцов все возможные, не совпадающие со столбцами матрицы (4), комбинации 3-разрядного двоичного кода. Очевидно, что данным условиям удовлетворяют несколько вариантов построения 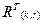, отличающиеся расположением различных столбцов, причём все эти варианты порождают эквивалентные (т.е. имеющие одинаковые минимальное кодовое расстояние и исправляющую способность) коды. Рассматривая столбцы как запись десятичных чисел в двоичной форме с условием, что верхний элемент столбца является старшим разрядом, при выполнении данной лабораторной работы для исключения отмеченной неоднозначности, будем располагать их слева направо в порядке, соответствующем убыванию значений десятичных чисел. (Такой подход использовался при составлении вариантов задания). В нашем примере это приводит к результату:

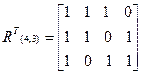. (5)

Объединяя (5) и (4) в соответствии с (2), получаем:

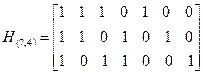. (6)

Транспонирование матрицы 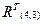приводит к результату:

, (7)

а единичная матрица выглядит так:

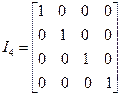. (8)

Объединяя (8) и (7) в соответствии с (3), получаем:

. (9)

Для выполнения последующих пунктов рабочего задания целесообразно воспользоваться возможностями пакета Matlab в интерактивном режиме. При этом сформированные матрицы в командном окне системы Matlab задаются как:

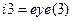; %формируем матрицу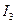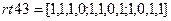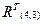

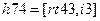; %формируем матрицу

; %формируем матрицу

; %формируем матрицу

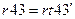; %формируем матрицу 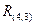(транспонируем )

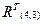%формируем матрицу

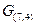
4.2. Кодирование (формирование разрешённой комбинации кода).

Кодирование, т.е. формирование кодовых слов 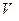систематического кода Хемминга сводится к умножению вектора , содержащего заданных информационных разрядов кода, на образующую матрицу 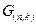., т.е

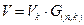. (10)

При этом умножение в (10) осуществляется с использованием правил выполнения арифметических операций в поле .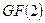

В качестве примера выполним кодирование кодом (7,4) информационной последовательности 1101. При этом , 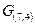задаётся соотношением (9), и в соответствии с (10) имеем:

.

Специфика вычислений в поле 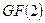в данном случае проявляется в том, что, например, при вычислении шестого слева разряда кодового слова 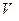имеем: , т.е. сложение выполняется по модулю 2, что соответствует правилам выполнения арифметических операций в поле .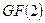

В командном окне пакета Matlab рассмотренные действия можно реализовать следующим образом:

v4g=gf([1,1,0,1]); %задаём информационный вектор в поле %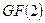

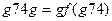; % задаём сформированную ранее матрицу 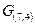в %поле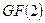

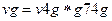; % вычисляем вектор сформированного слова %кода 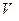в поле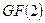

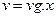; % переводим вычисленный в поле 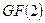вектор %сформированного слова кода 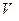в поле действительных чисел

Дата добавления: 2015-07-02