Декодирование принимаемой кодовой комбинации. 1 страница

Существуют различные методы декодирования кодов БЧХ. В настоящей лабораторной работе рассматривается алгебраический метод, основанный на использовании алгоритма Питерсона-Горенстейна-Цирлера [2].

Предположим, что при прохождении по каналу связи сформированная в п.4.2 комбинация 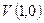вследствие воздействия помех превратилась в принимаемую кодовую комбинацию

1)

,

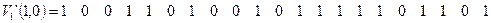
т.е. произошла одна ошибка в 22-м разряде (если считать первым−младший, крайний справа разряд), что соответствует полиному ошибок ;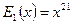

2)

,

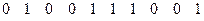т.е. произошло две ошибки в 29-м и 5-м разрядах, что соответствует полиному ошибок 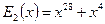. (Отметим, что в реальной ситуации, моделируемой в лабораторной работе, переданная комбинация и вид многочлена ошибок неизвестны.)

Процедуре определения количества ошибок и их исправления предшествует процесс вычисления синдрома принятой кодовой комбинации. Как известно [2], код синдрома 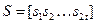состоит из 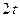элементов 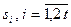, которые могут быть рассчитаны в расширении поля 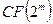как

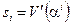, (5)

где 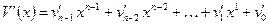− многочлен над полем 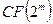, соответствующий принимаемой кодовой комбинации 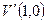; 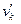− значение 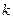-го разряда (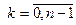) кода 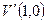; 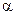− примитивный элемент поля .

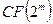Вычисления по формуле (5) удобно выполнить, используя возможности, представляемые пакетом Matlab. Для этого необходимо:

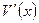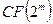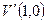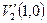1) в командном окне системы Matlab задать полином над полем , соответствующий принимаемой комбинации . Для двух рассматриваемых нами случаев приёма и (при 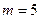) это можно сделать с использованием команд

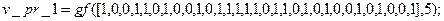
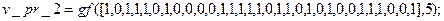
2) задать вектор 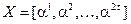набора степеней примитивного элемента 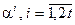расширения поля 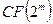, которые в соответствии с (5) представляют собой значения аргументов 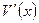при вычислении 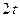элементов синдрома 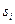. При этом следует использовать десятичные представления элементов 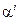(см. Табл. П.3, и П.4). В рассматриваемом примере (при 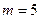, 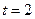) этот вектор задаётся командой

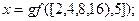
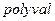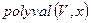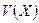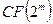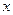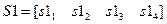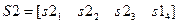3) с использованием команды , вычислить вектор элементов синдрома. Команда , позволяет оценить значение многочлена в расширении поля , которому принадлежат задаваемые в качестве аргумента значения . В нашем примере для расчёта векторов элементов синдрома и в командном окне системы Matlab следует записать:

;

;

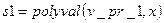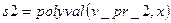Выполнение этих команд даёт следующие результаты:

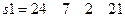; (6)

. (7)

Каждое из полученных чисел отражает собой десятичное представление значения соответствующего элемента синдрома в поле 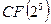, т.е. . Отметим, что, если принятая комбинация не содержит ошибок, вектор синдрома будет содержать одни нули. В этом можно убедиться, вычислив синдром сформированной ранее передаваемой кодовой комбинации 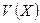, выполнив команды

.

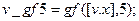
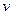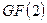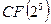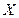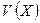Первая из этих команд позволяет по полученному ранее многочлену над полем сформировать соответствующий ему многочлен над расширением поля , а вторая − оценить значение этого многочлена при заданном векторе входных аргументов . В результате этого оценивания получается нулевой синдром , т.е. = 0.

Поскольку вектор элементов синдрома мы определяли как 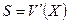, а 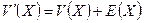, причём 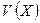= 0, то должно выполняться следующее соотношение:

(8)

где

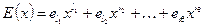− (8a)

многочлен ошибок, содержащий 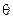слагаемых вида 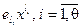, каждое из которых соответствует наличию ошибки на позиции 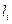, имеющей ненулевое значение (индекс 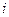обозначает номер ошибки, а индекс 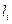−расположение 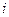-й ошибки в кодовом слове);

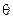−количество ошибок в принятой кодовой комбинации.

При этом выражение, определяющее вычисленный ранее (с использованием 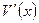), например, первый элемент синдрома 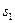на основании (8) с учётом (8a) можно записать как результат вычисления значения полинома 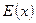при :

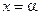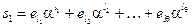. (9)

Вводя в рассмотрение величины локаторов ошибок 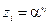и новые обозначения для величин ошибок 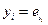соотношение (9) можно представить в виде:

.

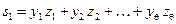Аналогичным образом, вычисляя значения 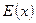при 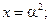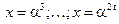, получаем выражения, определяющие остальные элементы 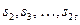синдрома, например, 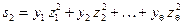и т.д. Совокупность этих выражений можно рассматривать как систему, содержащую 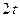нелинейных уравнений с неизвестными и 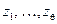. Решение этой системы, т.е. определение значений и 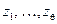, и составляет проблему декодирования принятой комбинации с исправлением присутствующих в ней ошибок. Вместе с тем нелинейность входящих в состав системы уравнений делает эту задачу весьма сложной. Рассмотрим способ её решения, называемый алгоритмом Питерсона-Горенстейна-Цирлера.

В соответствии с этим алгоритмом вводится в рассмотрение полином локаторов ошибок 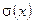, определяемый следующим образом:

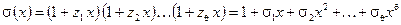. (10)

Как видно из первого из равенств (10), корнями многочлена 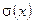будут величины 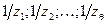, обратные значениям локаторов ошибок 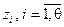, определяющих позиции расположения ошибок в полиноме 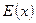. Определение коэффициентов полинома (10) осуществляется на основе авторегрессионной техники моделирования[2,4], в соответствии с которой составляется матричное уравнение, связывающее предшествующие 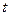значений элементов синдрома с последующим. В общем виде это уравнение выглядит так:

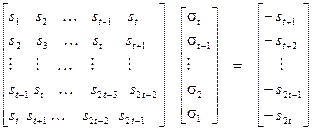(11)

Поскольку для элементов конечных полей справедливо равенство 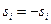при любых 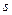и 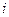, знаком «−» в правой части соотношения (11) можно пренебречь.

Соотношение (11) записано в предположении, что число ошибок 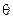, присутствующих в анализируемой кодовой комбинации, равно исправляющей способности кода 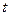. При этом определитель 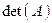матрицы должен быть отличен от нуля. В случае, если 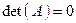, матричное уравнение (11) не имеет решения. Это говорит о том, что порядок полинома локаторов (а, следовательно, и число ошибок) 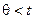. В такой ситуации следует уменьшить на 1 число строк и столбцов квадратной матрицы 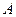(убрать последние строку и столбец), сократив соответствующим образом и размерность двух других присутствующих в (11) матриц (векторов-столбцов). В итоге соотношение (11) трансформируется к виду:

.

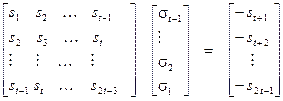Данную процедуру следует выполнять до тех пор, пока определитель преобразованной матрицы 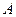не станет отличным от нуля. При этом зафиксированное в этом случае количество строк (или столбцов) этой матрицы и определяет число ошибок в анализируемой комбинации.

Возвращаясь к рассматриваемым примерам, в которых для кода (31,21), 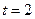на основании (11) можно записать:

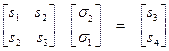. (12)

После подстановки в (12) найденных ранее значений элементов синдрома (6) в первом рассматриваемом примере это уравнение принимает вид:

1) 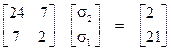. (13)

Напомним, что фигурирующие в выражении (13) числа отражают десятичное представление элементов поля 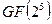. Для вычисления определителя матрицы 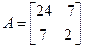воспользуемся возможностями системы Matlab, записав следующие команды:

;

.

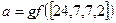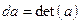Первая из этих команд задаёт матрицу 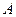в поле 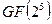, а вторая − вычисляет её определитель и возвращает в рассматриваемом примере значение da, равное 0. Это позволяет сделать вывод о том, что в анализируемой кодовой комбинации присутствует менее двух ошибок, т.е. одна ошибка. (О её наличии говорит тот факт, что синдром (6) данного блока кода является ненулевым вектором). В соответствии с приведёнными выше рекомендациями преобразуем соотношение (13) к виду:

,

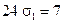откуда с использованием таблицы П.4 получаем:

.

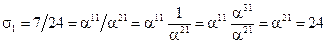Найденное значение 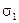позволяет записать полином локаторов ошибок в виде:

или .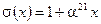

Корень 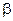этого полинома (значение 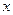, при котором 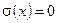) нетрудно определить из уравнения , откуда 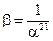. Данному корню соответствует значение локатора ошибок 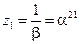, который указывает, что единственная ошибка в кодовой комбинации 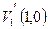находится на позиции, соответствующей 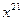в многочлене 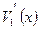. Поскольку рассматриваемый код является двоичным, для исправления этой ошибки достаточно изменить значение 22-го разряда (если считать первым−младший, крайний справа разряд) комбинации 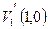с 1 на 0. При этом принимаемый кодовый блок 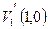превращается в переданную комбинацию .

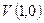Во втором из рассматриваемых примеров после подстановки в (12) найденных ранее значений элементов синдрома (7) это уравнение принимает вид:

2) 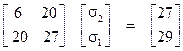(14)

В данном случае матрица 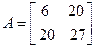, вводимая в командном окне системы Matlab оператором

; (15)

имеет ненулевой определитель 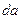, вычисляемый по команде

.

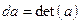Это говорит о том, что матричное уравнение (14) имеет решение и в исследуемой комбинации 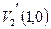присутствует ошибки.

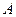Для решения уравнения (14) нужно обе его части умножить слева на матрицу , обратную матрице . При этом получим:

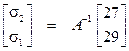, (16)

откуда могут быть определены значения 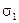и 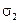. Процедуры обращения матрицы и матричного умножения в поле 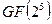целесообразно выполнить с использованием возможностей системы Matlab. Поскольку матрица 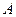была уже введена оператором (15), для её обращения (т.е. получения матрицы ) достаточно выполнить команду

.

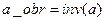Затем необходимо ввести значение второго сомножителя правой части выражения (16) и выполнить перемножение матриц. Это делается с использованием следующих операторов:

;

.

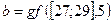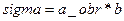В результате их выполнения получаем: 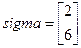. Подставляя этот результат в выражение (16), имеем:

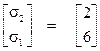, откуда имеем и .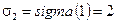

Найденные значения 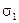и 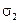позволяют записать полином локаторов ошибок в виде: . В отличие от первого примера в данном случае порядок этого полинома равен 2, поэтому процедура определения его корней в поле 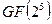является более сложной. Для её выполнения необходимо поочерёдно вычислять значения полинома, подставляя вместо 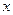все ненулевые значения элементов поля 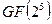до тех пор, пока при двух из них (которые и являются корнями) не получим 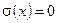. Удобнее эту операцию выполнить с использованием возможностей системы Matlab, записав следующие команды:

;

.

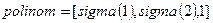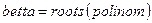В результате их выполнения получаем: 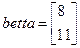.Для нахождения значений локаторов ошибок 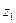и 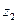необходимо вычислить величины, обратные значениям найденных корней. Это нетрудно сделать, воспользовавшись данными табл. П.3 или с помощью команды Matlab

.

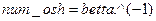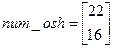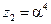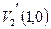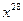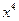В результате её выполнения выводятся значения , которые в степенном представлении (см. табл.П.3) соответствуют значениям и . Это указывает на то, что ошибки в кодовой комбинации находится на позициях, соответствующих и в многочлене 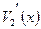. Поскольку рассматриваемый код является двоичным, для исправления этих ошибок достаточно изменить значения 29-го и 5-го разрядов (если считать первым−младший, крайний справа разряд) комбинации 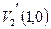с 1 на 0. При этом принимаемый кодовый блок 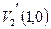превращается в переданную комбинацию .

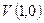4.4. Краткое описание алгоритма моделирующей программы и методики работы с ней.

Блок-схема алгоритма моделирующей программы остаётся такой же, как и в лабораторной работе №1 и представлена на рис.1.1. методических указаний к работе №1.

Методика работы с программой также остаётся прежней (изложенной в п.4.4 методических указаний к работе №1) за исключением того, что в отличие от работы 1 в данном случае в ответ на запрос “Введите значение исправляющей спосбности t =” следует вводить различные значения 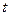, указанные в таблице П.1.2 в соответствии с вариантом задания.

Контрольные вопросы

1. Изложите методику определения порождающего многочлена кода БЧХ.

2. Изложите методику кодирования с использованием кода БЧХ.

3. Поясните назначение и методику определения многочлена 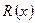при кодировании с использованием кода БЧХ.

4. Что такое синдром?

5. Изложите методику определения синдрома.

6. Поясните правило определения десятичного представления элементов 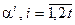расширения поля .

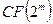7. Поясните идею составления системы, содержащей 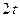нелинейных уравнений с неизвестными и 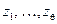, решаемую методом Питерсона-Горенстейна-Цирлера.

8. Что такое многочлен локаторов ошибок?

9. Как определяются коэффициенты многочлена локаторов ошибок?

10. Как определяется число ошибок в принятой кодовой комбинации?

11. Как определяется местонахождение ошибок в принятой кодовой комбинации и как они исправляются?

12. Какими параметрами задаётся код БЧХ?

13. Как построена моделирующая программа (привести ее алгоритм)?

14. Как оценивается вероятность ошибки в дискретном канале (без кодека)?

15. Как оценивается вероятность ошибки в системе с кодеком?

16. Как зависит вероятность ошибки в системе с кодеком от исправляющей способности и скорости кода?

Литература

1.Конспект лекций по ПДС.

2. Блейхут Р. Теория и практика кодов, контролирующих ошибки.− М. «Мир», 1986 г.

3. Султанов Б.В., Иванов А.П. Геращенко С.М. Математические основы построения помехоустойчивых блочных кодов. Учебное пособие. ПГУ, 2006

4. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. М.: Издательский дом «Вильямс», 2003 г.

Приложение

Таблица П.1.1. Варианты заданий к п. 2 − 4 лабораторной работы 2.

№ вар.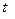

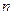
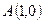
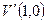
Дата добавления: 2015-07-02