Преобразование Лапласа и его основные свойства

Операторный метод анализа переходных процессов.

В основе операторного метода лежит преобразование Лапласа и операционное исчисление, известные из курса высшей математики. Операторный метод позволяет производить анализ переходных процессов при воздействии сигналов любой формы и не требует определения постоянных интегрирования, что существенно упрощает анализ электрических цепей, порядок которых выше чем первый.

Пусть f(t) - функция действительного переменного t, которая удовлетворяет следующим условиям:

f(t) тождественно равно нулю при t <0;

f(t) - однозначная кусочно-непрерывная функция с конечным числом разрывов первого рода;

При t > 0 функция f(t) растет не быстрее чем экспонента, т.е.

, где M ₀ и S ₀ - положительные действительные числа.

Указанным условиям удовлетворяют практически все функции времени, используемые в электротехнических задачах. При этих условиях существует интегральное преобразование Лапласа от функции f(t):

,

(3.1)

где f(t) - оригинал; F(p) - изображение исходной функции; 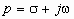- комплексная переменная.

Таким образом преобразование Лапласа устанавливает взаимно однозначное соответствие между исходной функцией времени f(t) и другой функцией другой (комплексной) переменной F(p). Для обозначения того, что эта пара функций связаны преобразованием Лапласа (3.1) будем использовать краткую запись или .

Рассмотрим некоторые свойства преобразования Лапласа, необходимые для дальнейшего рассмотрения операторного метода. Доказательство их проводится в соответствующем курсе математики.

1. Линейность преобразования: изображение суммы функций равно сумме изображений слагаемых.

Если и , то

,

(3.2)

где к₁ и к₂ - вещественные числа.

Это свойство следует непосредственно из определения преобразования (3.1) и может быть распространено на произвольное число слагаемых.

2. Дифференцирование оригинала.

Если , то ,

(3.3)

где - производная, f( 0 ) - начальное значение исходной функции.

При нулевых начальных условиях (f( 0 ) = 0) имеем простое соотношение: .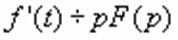

3. Интегрирование оригинала.

Если 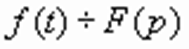, то

(3.4)

4. Теорема запаздывания.

Если 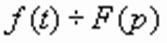, то

(3.5)

5. Произведение изображений.

Если и , то

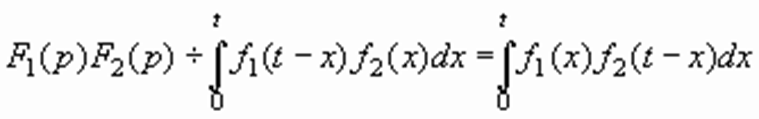
(3.6)

Интегралы в правой части называют сверткой функций. Произведение изображений соответствует свертке оригиналов. Свертка двух функций соответствует произведению их изображений.

Дата добавления: 2015-07-02