Метод преобразования схемы

В ряде случаев расчет сложной схемы, состоящей из линейных сопротивлений, существенно упрощается, если в этой схеме заменить группу сопротивлений другой эквивалентной группой сопротивлений, в которой сопротивления соединены иначе, чем в замещаемой группе. Взаимная эквивалентность двух групп сопротивлений выразится в том, что после замены электрические условия во всей остальной схеме не изменятся.

Условия эквивалентности звезды и треугольника проще всего определяются посредством сопоставления межузловых сопротивлений и проводимостей двух этих схем. Возьмем некоторый источник напряжения и присоединим к нему сначала узлы А и В

треугольника (рис.1-3), затем – одноименные узлы звезды. В случае эквивалентности треугольника и звезды в обоих случаях сила тока I_a, которой будет нагружен источник, должна быть одинакова, что будет иметь место, если одинаковы проводимости, а следовательно, и сопротивления между узлами А и В треугольника и звезды. Это равенство сопротивлений должно иметь место также при включении к источнику энергии узлов В и С, а затем и узлов С и А.

Проводимость между узлами А и В треугольника складывается из проводимости стороны А – В, равной 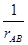, и проводимости, образуемой соединенными последовательно по отношению к узлам А, В сторон ВС и СА. Эта проводимость будет . Следовательно, общая проводимость между узлами А и В треугольника равна:

Сопротивление между узлами А, В треугольника – величина, обратная проводимости между этими узлами, т.е. оно равно:

При соединении звездой сопротивление между теми же узлами А, В будет равно сумме сопротивлений двух соответствующих лучей звезды, т.е. оно будет равно .

Согласно условию эквивалентности должно иметь место равенство

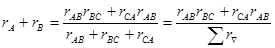(3-1)

здесь -- сумма сопротивлений всех трех сторон треугольника.

Структура схем звезды и треугольника по отношению к узлам симметрична, поэтому уравнения равенства сопротивлений для узлов В, С, а затем и для узлов С, А можно получить из (3-1) путем простой циклической перестановки индексов:

(3-2)

(3-3)

Чтобы определить , сложим (3-1) и (3-3) и вычтем из этой суммы (3-2); разделив последнюю на 2, найдем:

(3-4)

Два остальных уравнения получим путем простой циклической перестановки индексов в правой части:

(3-5)

(3-6)

При некоторых расчетах целесообразно осуществить обратное преобразование звезды в эквивалентный треугольник. Чтобы составить уравнения для такого преобразования, перемножим попарно выражения (3-4), (3-5), (3-6) и, сложив полученные произведения, получим:

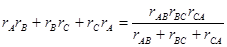
затем последнее выражение разделим на (3-6) и таким путем определим:

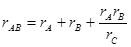(3-7)

после чего посредством циклической перестановки индексов найдем выражения сопротивлений остальных двух сторон эквивалентного треугольника:

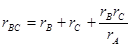(3-8)

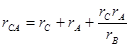(3-9)

Дата добавления: 2015-07-02