Метод узловых потенциалов

Метод узловых потенциалов позволяет уменьшить число совместно решаемых уравнений. Метод основан на применении первого закона Кирхгофа и заключается в следующем:

1) один узел схемы цепи принимаем базисным с нулевым потенциалом. Такое допущение не изменяет значения токов в ветвях, так как ток в каждой ветви зависит только от разностей потенциалов узлов, а не от действительных значений потенциалов;

2) для остальных узлов составляем уравнения по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов;

3) решением составленной системы уравнений определяем потенциалы узлов относительно базисного, а затем токи ветвей по обобщенному закону Ома.

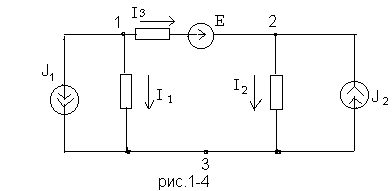Рассмотрим применение метода на примере расчета цепи по рис. 1-4, содержащей 3 узла. Узел 3 принимаем базисным, т.е. 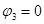. Для узлов 1 и 2 уравнения по первому закону Кирхгофа:

узел 1

узел 2

где

после подстановки

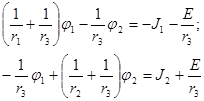(4-1)

Решение системы уравнений (4-1) методом подстановок определяет потенциалы узлов, а следовательно, и токи ветвей. Из записи (4-1) очевиден принцип составлений уравнений по методу узловых потенциалов. В левой части уравнений коэффициент при потенциале рассматриваемого узла положителен и равен сумме проводимостей сходящихся к нему ветвей. Коэффициенты при потенциалах узлов, соединенных ветвями с рассматриваемым узлом, отрицательны и равны проводимостям соответствующих ветвей.

Правая часть уравнений содержит алгебраическую сумму токов ветвей с источниками токов и токов короткого замыкания ветвей с источниками ЭДС, сходящихся к рассматриваемому узлу, причем слагаемые берутся со знаком плюс (минус), если ток источника тока и ЭДС направлены к рассматриваемому узлу (от узла).

В частном случае схемы замещения без источников тока с двумя узлами потенциал узла 1 при базисном узле 2, т.е. при 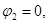равен напряжению между узлами

(4-2)

Выражение (4-2) называется формулой межузлового напряжения. Например, для цепи на схеме рис.1-5 напряжение между узлами по (4-2)

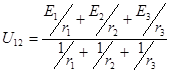
Дата добавления: 2015-07-02