Подання чисел в ЕОМ із плаваючою комою

При використанні чисел з плаваючою комою у розрядну сітку машини записується не тільки саме число в деякому масштабі, але і сам масштаб цього числа. У напівлогарифмічній формі подання будь-яке число x має вигляд: x=S^P·M, де S – основа системи числення, Р – ціле число, що називають порядком, М - мантиса числа, | M | <1.

У розрядну сітку числа звичайно записується не сама степінь основи S^P, а тільки порядок P і мантиса числа M. Наприклад, число у = 24.12 у напівлогарифмічній формі в звичайній десятковій системі числення буде мати вид: у = 10² × 0,2412 або y = 10³ × 0,02412 і т.п.

Як правило, число в форматі з плаваючою комою повинно бути нормалізоване, тобто мантиса повинна знаходитись в діапазоні 0,1≤|M|<1. Наприклад, число 10³·0,02412 не нормалізоване, в мантисі після коми повинно бути будь-яка цифра, тільки не 0. Нормалізація: 10³·0,02412 = 10²·0,2412 – при перенесенні коми в мантисі вліво – порядок зменшується на 1, вправо - збільшується.

Оскільки масштаб числа при його записі в напівлогарифмічній формі записується в розрядну сітку машини, то операції запам'ятовування, вирівнювання масштабів (порядків) і т.п. виконуються машиною і не потребують особистої участі з боку людини. Правда, після виконання операцій може потребуватися нормалізація мантиси і відповідна зміна порядку. Але ці операції досить просто реалізуються в машині.

При виконанні операцій над числами, поданими у формі з плаваючою комою, можливо одержання результату, порядок котрого більше припустимого в машині. Це також варто враховувати при проведенні обчислень. Наприклад, нехай потрібно обчислити z = w×v/u, причому w = 10¹⁰ × 0,4, v = 10⁸ × 0,3 і u = 10⁸ × 0,2, а максимально припустимий порядок у машині 10¹². Якщо спочатку підрахувати множення w × v, то відбудеться так зване переповнення один по одному і машина припинить обчислення. Якщо ж спочатку виконати операцію ділення у = w/u, а потім множення y × v, одержимо потрібний результат.

При поданні чисел у напівлогарифмічній формі також виникає проблема кодування знака. Вона вирішується так само, як і для поданні чисел у формі з фіксованою комою, але додаткових розрядів потрібно вже два – для знака порядку і знака мантиси.

Розглянемо як приклад розрядну сітку для представлення двійкових чисел у 32 розрядах.

Розрядна сітка машини з плаваючою комою (з урахуванням розрядів під знаки мантиси і порядку)

Нехай запис числа має вигляд: 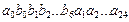. Перші два розряди виділяються під знаки мантиси (числа) і порядку відповідно, розряди з 3-го по 8-й виділяються під запис модуля порядку, а 24 розряди з 9-го по 32-й – під запис модуля мантиси. Тоді діапазон подання чисел буде визначатися в такий спосіб: 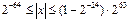, що приблизно відповідає діапазону чисел від 10^-19 до 10¹⁹.

Як уже відзначалося, форма подання з плаваючою комою є основною формою подання чисел у сучасних обчислювальних машинах. До її недоліків відносять зменшення продуктивності машини в порівнянні з обчисленнями в природній формі, ускладнення її технічних пристроїв. Наприклад, повинні бути розроблені схеми нормалізації, передбачене устаткування для виконання операцій над порядками і мантисами чисел і т.п. Обчислювальні машини, у яких може бути використана і та й інша форми подання, дозволяють врахувати особливості розв'язуваної задачі і підвищити продуктивність обчислень.

╔═··· Приклад 1. Число х=222,24 подати в комп’ютерній формі подання в форматі з фіксованою точкою. Для зображення чисел в уявній ЕОМ використовувати двобайтне слово. Який при цьому може бути масштаб числа, щоб точність числа була найбільшою?

Переведемо число в 2-ву СЧ: х=222,24=11011110,00111101₂.

Слово довжиною в 2 байти містить 16 розрядів для зображення числа, причому крайній лівий 0-й розряд відводиться під знак. Отже для зображення числа відведено 15 розрядів, з 1-го по 15-й.

Для числа x повинен бути введений відповідний масштаб M_x, так що добуток M_x×x потрапив в прийнятий діапазон зображення чисел, тобто, щоб | M_x×x |<1 треба перенести кому в числі х на 10 розрядів вліво, тобто помножити на 2^-10. Одже M_x =2^-10.

№ розрядів

Код числа

╚═···

╔═··· Приклад 2. Число х=222,24 подати в комп’ютерній формі подання в форматі з плаваючою точкою. Для зображення чисел в уявній ЕОМ використовувати слово в 4 байти за приведеним зразком.

Переведемо число в 2-ву СЧ: х=222,24=11011110,00111101₂

Нормалізуємо число: х=11011110,00111101₂ =0,1101111000111101·10¹⁰.

Порядок р=10=1010₂, мантиса m=1101111000111101, знаки числа і порядку +, тобто кодуються 0.

№ розрядів

....

Код числа

....

Знак числа

порядок

мантиса

Знак порядку

╚═·· ·

Самостійна робота № 7

Тема: Арифметичні операції в кодах ЕОМ.

Мета: Закріпити набуті знання та навички, перевірити їх при виконанні практичних завдань.

Дата добавления: 2015-07-02