
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Дирихле (достаточный признак представимости функции рядом Фурье)
|
|
|
|
ТЕОРЕМА ДИРИХЛЕ
Определение 1. Функция 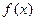 называется кусочно-непрерывной на
называется кусочно-непрерывной на 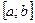 , если она непрерывна на этом промежутке или имеет на нем конечное число разрывов I рода.
, если она непрерывна на этом промежутке или имеет на нем конечное число разрывов I рода.
Определение 2. Функция 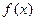 называется кусочно-монотонной на
называется кусочно-монотонной на 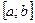 , если она монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна (т.е. функция на
, если она монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна (т.е. функция на 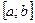 имеет конечное число экстремумов).
имеет конечное число экстремумов).
Определение 3. Говорят, что 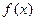 удовлетворяет условиям Дирихле на
удовлетворяет условиям Дирихле на 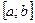 , если
, если 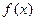 на
на 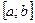 является кусочно-непрерывной и кусочно-монотонной.
является кусочно-непрерывной и кусочно-монотонной.
Если функция 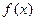 удовлетворяет условиям Дирихле на
удовлетворяет условиям Дирихле на 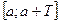 , то ряд Фурье для этой функции сходится на этом отрезке и при этом:
, то ряд Фурье для этой функции сходится на этом отрезке и при этом:
1. В точках непрерывности функции сумма ряда 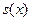 совпадает с самой функцией:
совпадает с самой функцией: 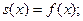
2. В каждой точке 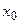 разрыва функции сумма ряда равна среднему арифметическому пределов функции
разрыва функции сумма ряда равна среднему арифметическому пределов функции 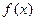 слева и справа:
слева и справа:
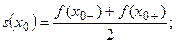
3. В точках 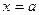 и
и 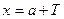 (на концах отрезка) сумме ряда равна
(на концах отрезка) сумме ряда равна
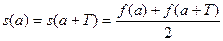 .
.
Замечания
1. Условиям Дирихле удовлетворяют многие функции, которые встречаются в математике и ее приложениях. Однако существуют функции, не удовлетворяющие условиям Дирихле, но при этом представимые рядом Фурье, т.е. теорема Дирихле дает лишь достаточное условие представимости, но не необходимое.
2. Теорема о периодическом продолжении функции.
Сумма ряда Фурье есть периодическая функция с периодом Т.
Доказательство
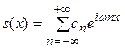
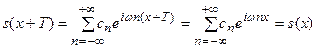 при любом х.
при любом х.
Т.о., график функции 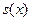 есть график периодической функции на всей числовой оси. Говорят, что
есть график периодической функции на всей числовой оси. Говорят, что 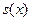 периодически продолжает на всю числовую ось функцию
периодически продолжает на всю числовую ось функцию 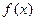 , заданную на
, заданную на 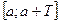 .
.
Пример 1. Разложить функцию 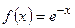 , заданную на отрезке
, заданную на отрезке 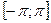 , в ряд Фурье в комплексной форме.
, в ряд Фурье в комплексной форме.
Решение. Данная функция в указанном интервале удовлетворяет условиям Дирихле.
По формулам (2) имеем 
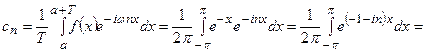
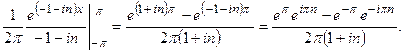
Т.к. 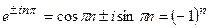 , то
, то 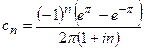 ,
,
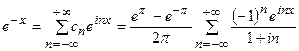 .
.
В интервале 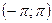 этот ряд представляет функцию
этот ряд представляет функцию 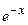 , а в точках
, а в точках  его сумма равна
его сумма равна 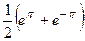 .
.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1985; Нарушение авторских прав?; Мы поможем в написании вашей работы!