Распределение характеристик качеств руководителей

Группа	ПОКАЗАТЕЛЬ
Уровень организаторских способностей	Уровень коммуникативных способностей	Выраженность лидерских качеств
низкий	средний	высокий	низкий	средний	высокий	слабо	средне	сильно	диктат
Г1	2/6	0/6	4/6	0/6	2/6	4/6	0/6	1/6	3/6	2/6
Г2	0/6	2/6	4/6	0/6	2/6	4/6	0/6	2/6	3/6	1/6
Г3	1/9	1/9	7/9	0/9	3/9	6/9	1/9	2/9	6/9	0/9
Г4	2/14	1/14	11/14	0/14	3/14	11/9	1/14	2/14	11/9	0/14
Общее значение уровня	5/35	4/35	26/35	0/35	0/35	25/35	2/35	7/35	23/35	3/35

Примечание.

Г1 – начальники цехов, Г2 – заместители, Г3 – старшие мастера,

Г4 – мастера.

Если какое-либо значение не встречается, то частота f = 0 все равно должна быть указана. В таблице 5 объединены три методики, дающие номинативное распределение признака, и четыре группы испытуемых. (Данные взяты из дипломной работы Балышевой Н.А., ИрГТУ). При описании таблицы мы можем сравнивать как признаки, так и группы между собой. Помимо этого, последняя строка дает общее по всем группам распределение признаков, и сразу можно видеть, что по первой методике преобладающие результаты высокие, а по двум другим средние.

Что касается графического представления частотного распределения, можно использовать как полигоны частот гистограммы, диаграммы и др. формы представления. Так гистограмма, выполненная в «STATISTIKA», будет выглядеть как на рис.1 (см. ниже пример 3 из подраздела «Интерпретация результатов корреляционного анализа» п. 2.3 «Анализ и интерпретация результатов»).

Гистограмма используется только для количественных переменных, когда значение признака представимо числом. Если этого сделать нельзя, можно использовать обычную столбиковую диаграмму (см. рис.2).

Рис.1. Пример гистограммы частотного распределения признака

Для того, чтобы получить гистограмму для данных, обрабатываемых программой STATISTIKA, необходимо в Basic Statistics выбрать окно Frequency tables. В нем выбираете длину шага (это автоматически делает программа, но вы можете, например, увеличить шаг и таким образом перегруппировать данные), и далее окно Histograms. Кстати, именно по гистограмме или полигону частот можно судить, какое именно у вас распределение: нормальное, бимодальное, равномерное или иное, что также имеет значение при интерпретации.

Если изучаемая переменная распределяется по достаточно большому числу интервалов, т.е. вас интересует даже незначительные ее изменения, то гистограмма более наглядно представит ваши данные. В противном случае можно использовать как гистограмму так и диаграмму, она выглядит более эффектно (см. рис. 2, 3)

Большой выбор различного вида графиков есть у программы EXEL в разделе Мастер диаграмм. Поэтому хорошо бы вам научиться переводить матрицу исходных данных из STATISTIKA в EXEL и наоборот. Эту операцию можно проделать различными способами, например, таким: выделить матрицу исходных данных, нажав на левую верхнюю иконку TEX VAL, скопировать ее, выбрав на панели Edit и Copy, открыть в своей папке новый файл типа Лист Microcoft Exel и перенести в него свою матрицу. Когда вы определили основные статистики и частотные распределения, можете считать, что ваши данные описаны. Далее надо приступать к следующему этапу обработки, а именно решению основных задач, которые связаны с анализом и доказательством исходной гипотезы.

Рис. 2. Ответственность за распределение времени

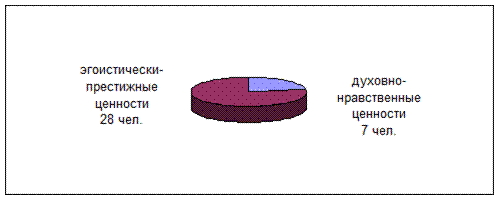
Рис. 3. Ценностная направленность респондентов

Хотелось бы сделать еще одно замечание о представлении частот данных. Чаще всего в студенческих работах предлагается %-ое распределение. Это более привычно для гуманитарного сознания, но это неверно. Если вспомнить, что % есть сотая часть чего-либо, то начинаешь понимать, что % имеет смысл при достаточно большой выборке, сопоставимой с объемом n=100 (например, 60-70 и более). Но если исследовательская выборка небольшая, то лучше представлять данные через частоты, абсолютные (28 ч. и 7 ч.) или относительные (28/35 и 7/35).

Дата добавления: 2015-07-02