Выпуклые функции

Функция f на интервале

1) выпукла (выпукла вниз), если

2) строго выпукла (строго выпукла вниз), если

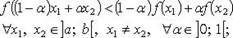
3) выпукла вверх, если

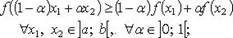
4) строго выпукла вверх, если

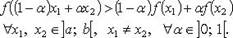
Признаки выпуклости дифференцируемых функций

1. Если f' возрастает на , то f выпукла на (если f' строго возрастает, то f строго выпукла).

2. Если , то f выпукла на (если 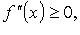обращаясь в нуль, возможно, лишь в конечном числе точек, то f строго выпукла).

3. Функция f выпукла тогда и только тогда, когда график функции лежит не ниже касательной, проведенной к нему в любой его точке.

Свойства выпуклых функций

1. В частности:

2.

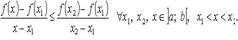
3. Точки любой дуги графика лежат под хордой, стягивающей эту дугу.

4. Функция f непрерывна на интервале и имеет в каждой его точке конечные односторонние производные.

5. Функция f имеет на не более одного локального минимума и не имеет локальных максимумов.

Точки перегиба

Пусть функция f определена в некоторой окрестности точки x₀, непрерывна в точке x₀ и имеет в этой точке конечную или бесконечную производную. Если при переходе через точку x₀ функция f меняет направление выпуклости, то x₀ называют точкой перегиба функции f, а точку (x₀; f(x₀)) - точкой перегиба графика функции f. График функции переходит с одной стороны касательной, проведенной в точке (x₀; f(x₀)), на другую сторону. Точки перегиба f - точки экстремума для f'.

Необходимые условия наличия перегиба

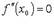либо 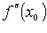не существует.

Достаточные условия наличия перегиба

1. Если меняет знак при переходе через точку x₀, то x₀ - точка перегиба.

2. Если 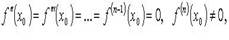то при n четном x₀ - точка перегиба, при n нечетном x₀ не является точкой перегиба.

Дата добавления: 2015-07-02