Долга: выплаты изменяются в арифметической 1 страница

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Задание 1 « Балансовая модель производства»

Задана матрица А коэффициентов прямых затрат

и вектор , представляющий собой план выпуска конечной продукции каждым экономическим объектом P_i системы (n =4).

Требуется найти:

а) матрицу S коэффициентов полных затрат 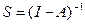, где I – единичная матрица размером n×n;

б) полный (валовой) выпуск продукции каждым экономическим объектом системы

;

в) план поставок между всеми экономическими объектами системы

, где ;

г) результаты расчётов свести в так называемую таблицу «затраты-выпуск» (таблица 1).

Таблица 1 – Таблица «затраты-выпуск»

Объекты	Р1	Р2	Р3	Р4	Конечный выпуск	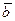Полный выпуск
Р1	Матрица Q
Р2
Р3
Р4

Указания:

Система балансовых уравнений в векторном виде

или .

Тогда

.

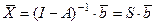В таблице 1 индицировать рассчитанные значения в целочисленном виде. На диаграмме изобразить конечный и валовой выпуск экономическими объектами системы.

Задание 2 «Выбор инвестиционного проекта»

Имеются два инвестиционных проекта, в которых потоки платежей на конец года характеризуются данными, представленными в таблице 1.

Таблица 1 – Потоки платежей по проектам

В тысячах рублей

Проект	Год
1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й
А	-200	-300						–
Б	-400	-100

Ставка сравнения (норматив рентабельности) принята в размере i =10%. Требуется выбрать более предпочтительный проект.

Указания:

Чистый приведенный эффект (доход) проекта (NPV – Net Present Value – чистая текущая стоимость) рассчитывается по формуле

,

где Р_к – денежные поступления в к-ом году;

IC_к – инвестиции в к-ом году;

i – ставка сравнения.

В нашем случае в таблице отражены денежные потоки . Из двух проектов более предпочтителен тот проект, который обеспечивает больший прирост капитала, т.е. у которого NPV выше.

Графически отобразить денежные потоки обоих проектов (в отдельности) по годам.

Задание 3 «Математика финансов: о наиболее выгодном

помещении капитала»

Вам встречаются два рекламных объявления: один банк предлагает r =15,5% (годовых) ежеквартально, а другой – r =15,2% ежемесячно. Какое предложение лучше?

Указания:

Для ответа на данный и подобные вопросы вводится вспомогательное понятие – эффективная процентная ставка r_e. Если на основной вклад Р в течение года m раз начисляются сложные проценты (ежеквартально – m =4; ежемесячно – m =12), то при годовой процентной ставке r ожидаемый вклад S через год составит

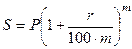. (1)

Эффективная процентная ставка r_e определяется из условия

, (2)

т.е. это простой процент, начисляемый за год лишь один раз и дающий такой же результат, что и сложные проценты с начислением m раз в году.

Из (1) и (2) следует, что

. (3)

В отличие от эффективной ставки r_e первоначальная ставка r с m -кратным начислением называется номинальной. Выгоднее тот вклад, у которого эффективная ставка r_e выше. Предусмотреть графическое отображение результатов и логический вывод: какое же помещение капитала выгоднее, например «таким образом, 15,5% ежеквартально даёт (больший, меньший или равный) годовой доход, чем 15,2% ежемесячно».

Задание 4 «Оптимальное размещение инвестиций: проекты, не

поддающиеся дроблению»

Фирма планирует инвестировать в основные фонды не более IC₀ =60 млн.руб.; цена источников финансирования составляет i =10%. Рассматриваются четыре альтернативных проекта со следующими потоками платежей (млн.руб.):

Проект А: -35; 11; 16; 18; 17.

Проект Б: -25; 9; 13; 17; 10.

Проект В: -45; 17; 20; 20; 20.

Проект Г: -20; 9; 10; 11; 11.

Необходимо составить оптимальный план размещения инвестиций, имея в виду, что к реализации могут быть приняты проекты только в полном объёме.

Указания:

В случае, когда инвестиционный проект может быть принят только в полном объёме, для нахождения оптимальных вариантов производят просмотр сочетаний проектов с расчётом их суммарного NPV. Чистая текущая стоимость (Net Present Value) проекта рассчитывается по формуле:

,

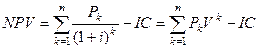где – коэффициент дисконтирования (дисконтный множитель).

Комбинация, обеспечивающая максимальное значение суммарного NPV, считается оптимальной.

Для расчёта NPV для каждого проекта необходимо составить таблицу, подобную таблице 1.

Таблица 1

Год	Коэффициент дисконтирования по ставке i	Проект А	…	Проект Г
Денежный поток, млн.руб.	Дисконтированные члены денежного потока, млн.руб. (гр.2хгр.3)	…	… (гр.2хгр.9)
1	2	3	4		9	10
0-й	1	-IC			-IC
1-й	V^1	P1			P1
2-й	V^2	P2			P2
3-й	V^3	P3			P3
4-й	V^4	P4			P4
NPVA = Σ	…	NPVГ = Σ

Возможные сочетания проектов и их суммарный NPV представить в таблице вида таблицы 2.

Таблица 2

Варианты сочетания проектов	Суммарные инвестиции ICΣ	Суммарный NPV
А	ICΣ= ICА	Если ICΣ≤ IC0, то отображать ΣNPV; в противном случае отображать сооб-щение «Сочетание невозможно»
…	…
А+Б	ICΣ= ICА+ ICБ
…	…
А+Б+В	ICΣ = ICА+ ICБ+ ICВ
…	…
А+Б+В+Г	ICΣ= ICА+ ICБ+ ICВ+ ICГ

Оптимальным является сочетание проектов ….

Графически отобразить денежные потоки проектов.

Задание 5 «Выявление основной тенденции»

На основе фактических среднегрупповых данных определить основную тенденцию изменения себестоимости (найти «кривую освоения») некоторого изделия, начиная с первого года выпуска (таблица 1).

Таблица 1

	Годы t выпуска продукции
Сt	`13,5	12,7	12,0	11,9	11,5	11,2	10,8	10,75	10,6	10,5

Получить «кривую освоения» методом наименьших квадратов в виде линейной функции , где – расчётные значения; – фактические значения. Параметры а и b находятся из следующей системы, полученной МНК-методом:

Среднелинейная ошибка отклонения ε расчётных уровней от фактических рассчитывается по формуле:

.

Указания:

Расчётная таблица имеет вид таблицы 2.

Таблица 2 – Расчётная таблица

№ п/п	Сt	yt	t	t^2	ytt
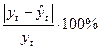
	13,5
	12,7
…	…
	10,5
–	–	Σ	Σ	Σ	Σ	–	–	Σ

На графике отобразить фактические данные и кривую освоения изделия.

Задание 6 «Задача целочисленного линейного программирования»

В плановом году строительные организации города переходят к сооружению домов типа Д₁, Д₂, Д₃, Д₄. Данные о количестве квартир разного типа в каждом из указанных типов домов, их плановая себестоимость и годовой план ввода жилой площади приведены в таблице 1.

Таблица 1

Тип квартир	Тип домов	Годовой план
Д1	Д2	Д3	Д4
Однокомнатная			–
Двухкомнатная	–
Трёхкомнатная
Четырёхкомнатная
Плановая себесто-имость, у.д.е.	26,7	34,9	40,6	30,1	–

Исходя из необходимости выполнения плана ввода квартир (а возможно, и его перевыполнения), найти план строительства домов на финансовый год, при котором общая себестоимость всех вводимых домов будет минимальной.

Указания:

Данная задача является ЗЛП целочисленного типа и может быть решена в среде Excel с помощью команды Сервис–Поиск решения… и работой с окном Поиск решения. Условие задачи вместе с исходными данными должно быть на первом рабочем листе; на втором рабочем листе должны отображаться данные, необходимые для окна Поиск решения, и результаты решения ЗЦЛП. Предусмотреть вывод информации о перевыполнении плана по вводу квартир (на том же рабочем листе). На третьем рабочем листе (или отдельном листе диаграмм) предусмотреть вывод диаграммы, отображающей план строительства домов типа Д₁, Д₂, Д₃ и Д₄ на финансовый год.

Задание 7 «Амортизация станка методом «суммы лет»»

Первоначальная (балансовая) полная стоимость станка составляет 45000 тыс.руб., ликвидационная стоимость – 4500 тыс.руб. Нормативный срок службы станка составляет 6 лет.

Определить суммы амортизационных отчислений на реновацию станка методом «суммы лет» (кумулятивным методом), если известно, что остаточная стоимость станка после 6-ти лет его эксплуатации должна равняться ликвидационной стоимости станка, т.е. стоимости лома и материалов.

Указания:

Результаты расчётов оформить в виде таблицы 1.

Таблица 1

Годы	Первоначальная (балансовая) стоимость станка, тыс.руб.	Остаточная стоимость станка на начало года, тыс.руб.	Норма амортиза-ционных отчислений Nai, %	Сумма амортиза-ционных отчислений Ai, тыс.руб.	Текущая сумма амортиза-ционного фонда ΣAi, тыс. руб.	Остаточная стоимость станка на конец года, тыс.руб.
	П
…	…	…	…	…	…	…
	П					Л

Здесь П – первоначальная (балансовая) стоимость станка;

Л – ликвидационная стоимость станка;

Т_н – нормативный срок службы станка;

Ч=1+2+…+(Т_н–1)+ Т_н = 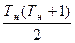– число суммы лет;

Na_i = – норма амортизационных отчислений, %;

А_i = Na_i(П–Л);

О_i^н = О_i-1^к – остаточная стоимость станка на начало i-го года эксплуатации;

О_i^к = О_i^н – A_i – остаточная стоимость станка на конец i-го года эксплуатации;

О₁^н=П.

Задание 8 «Погашение займа переменными выплатами основного

прогрессии»

Кредит размером D =4,0 млн.руб. выдан на n =5 лет под 15% годовых, т.е. i =0,15, с начислением процентов в конце каждого расчётного периода (года). Выплаты основного долга должны возрастать ежегодно на d =0,1 млн.руб.

Требуется составить план погашения кредита.

Указания:

Предположим, что контрактом предусмотрено погашение основного долга производить платежами, возрастающими или убывающими в арифметической прогрессии с разностью d. В этом случае выплаты основного долга составят:

1-й год – R₁ = R₁;

2-й год – R₁±d = R₂;

3-й год – R₁±2d = R₃;

…

n -й год – R₁±(n–1)d =R_n, т.е. R_к = R₁±(к–1)d,

где – для возрастающей прогрессии;

– для убывающей прогрессии.

Процентный платёж I_к=D_кi,

где D_к = D_к-1– R_к-1 – остаток основного долга в начале к -го периода (D₁ = D).

Годовая срочная уплата Y_к = I_к + R_к.

План погашения представить в табличной форме (таблица 1).

Таблица 1 – План погашения займа переменными выплатами основного долга (выплаты увеличиваются в арифметической прогрессии)

Год	Величина долга Dк	Процентный платёж Iк	Годовой расход по погашению основного долга Rк	Годовая срочная уплата Yк
1-й	D1	I1	R1	Y1
2-й	D2	I2	R2	Y2
3-й	D3	I3	R3	Y3
4-й	D4	I4	R4	Y4
5-й	D5	I5	R5	Y5
Итого	–	ΣIк	ΣRк	ΣYк

Проверка: ΣI_к + ΣR_к = ΣY_к; ΣR_к = D.

Графически отобразить Y_к.

Задание 9 «Анализ динамики фондоотдачи»

Имеются данные по двум отраслям (таблица 1).

Таблица 1

Отрасль	Объём продукции в постоянных ценах Q, млн.руб.	Среднегодовая стоимость основных производственных фондов Ф, млн.руб.
базисный период	отчётный период	базисный период	отчётный период
№1
№2

Определить:

а) динамику фондоотдачи по каждой отрасли и по двум отраслям вместе;

б) объём дополнительной продукции (∆Q), в том числе за счёт:

1) увеличения объёма основных производственных фондов (∆Q_ф);

2) изменения удельного веса основных производственных фондов с разным уровнем фондоотдачи (∆Q_{стр.сдв.});

3) изменения фондоотдачи по каждой отрасли (∆Q_f).

Указания:

Фондоотдача в рублях f=Q/Ф.

Динамику фондоотдачи характеризуют индексы:

– индивидуальные

– по двум отраслям вместе – индекс переменного состава

.

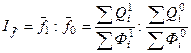Объём дополнительной продукции

,

причём

;

;

.

Контроль правильности расчётов:

Отобразить результаты графически.

Задание 10 «Формирование фонда погашения»

Фирма получила кредит D =5,0 млн.руб. на n =4 года под g =8% сложных годовых в банке А. Кредитный контракт предусматривает погашение долга разовым платежом. Одновременно с получением кредита фирма начала создавать погасительный фонд, для чего открыла счёт в банке Б. На размещённые средства банк Б начисляет i =10% годовых.

Требуется определить ежегодные расходы Y_t фирмы по амортизации долга при условии, что в погасительный фонд вносятся ежегодные равные суммы R.

Указания:

Параметры финансовой операции: D =5,0 млн.руб., g =8%; i =10%; n=N =4 года, где N – срок, на который рассчитано формирование погасительного фонда; Так как формирование фонда рассчитано на N лет, то вносимые в фонд платежи образуют ренту с параметрами R, N, i. Сумма данной ренты должна быть равна величине основного долга D (кредита), в силу чего можно записать: D=R^.S_N;i, откуда взнос в погасительный фонд . Величину процентного платежа I_t, исчислённого по сложным процентам, для расчётного периода t вычисляют по формуле 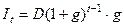. Накопления на конец года в погасительном фонде S_t рассчитываются по формуле S_t+1=S_t(1+i)+R, где t=1,2,…,N, причём S₀ =0. Величина срочной уплаты при начислении на основной долг D сложных процентов равна Y_t=I_t+R_t. План погашения кредита представить в виде таблицы 1.

Таблица 1 – План погашения кредита

В миллионах рублей

Год t	Выплата процентных платёжей It	Взносы в погасительный фонд Rt	Накопления на конец года в погасительном фонде St	Расходы по амортизации займа (срочные уплаты) Yt
	I1	R1	S1	Y1
	I2	R2	S2	Y2
	I3	R3	S3	Y3
	I4	R4	S4	Y4
Итого	ΣIt	ΣRt	–	ΣYt

Экономия фирмы по погашению долга за счёт создания погасительного фонда составляет ∆D=D(1+g)ⁿ–ΣY_t. Графически отобразить Y_t.

Задание 11 «Годовой процент начисления»

Подсчитать, на сколько процентов увеличится через год первоначальный вклад Р, равный единице, если процентная ставка r составляет 12% годовых соответственно ежегодно, ежеквартально, ежемесячно, два раза в месяц, еженедельно, ежедневно и ежечасно. Расчёты провести также для r =10 и 15% и построить графики (на одном рисунке) зависимостей годового процента начислений от количества периодов начислений процентов в году (n) для различных значений годовой процентной ставки r (r =10, 12 и 15%).

Указания:

Фраза «процентная ставка составляет 12% годовых ежеквартально» по общепринятой терминологии означает, что ежеквартально начисляется лишь четвёртая часть годовой ставки в 12%, т.е. 12%/4=3%, и, кроме того, подразумевается, что процент сложный, т.е. начисляется «процент от процента».

Сумма вклада через год рассчитывается по формуле:

. (1)

Годовой процент начислений определяется по формуле

. (2)

При вычислениях принять следующее: в году 52 недели, 365 дней и 8760 часов.

Для расчётов возможно использование финансовых функций.

При построении графиков 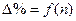принять по оси абсцисс логарифмический масштаб для отображения чисел n (от 1 до 8760).

Полученные данные представить в виде таблицы 1.

Таблица 1 – Годовая процентная ставка r =…%

Начисление сложного процента	n	Годовой процент начислений, %
ежегодно
ежеквартально
…	…
ежечасно

Задание 12 «Погашение долга равными срочными уплатами при

переменной процентной ставке»

Получен кредит в сумме D =10,0 млн.руб. сроком на n =7 лет. Процентная ставка (i) изменяется по годам в соответствии с таблицей 1.

Таблица 1

Годы	1–2	3–4	5–7
Процентная ставка	7,0	10,0	16,0

Погашение основного долга и выплата процентов происходит в конце года. Требуется составить план погашения долга при изменяющихся процентных ставках.

Указания:

D_к=D_к-1–R_к-1, к=1,…,n, причём D₀=D; R₀=0. Здесь D_к – остаток (сумма) долга на начало к -го года; R_к – сумма погашения основного долга, рассчитываемая по формуле: R_к=Y_к–I_к, где – годовая срочная уплата; I_к=D_к^.i – величина процентного платежа в конце к -го года.

План погашения долга представить в виде таблицы 2.

Таблица 2 – План погашения долга

В миллионах рублей

Год к	Процентная ставка iк	Сумма долга на начало года Dк	Сумма процентных денег Iк	Сумма погашения основного долга Rк	Годовая срочная уплата Yк
	0,07	D1	I1	R1	Y1
	0,07	D2	I2	R2	Y2
	0,10	D3	I3	R3	Y3
	0,10	D4	I4	R4	Y4
	0,16	D5	I5	R5	Y5
	0,16	D6	I6	R6	Y6
	0,16	D7	I7	R7	Y7
Итого	–	–	ΣIк	ΣRк	ΣYк

Проверка правильности расчётов: .

Дата добавления: 2015-07-02