Приближение (аппроксимация) функций (гармонический анализ)

Постановка задачи: Найти такой тригонометрический полином для кусочно-непрерывной на заданном интервале функции, который наилучшим способом приближал значения аппроксимируемой функции.

Решение задачи аппроксимации (гармонический анализ) – тригонометрический полином для функции () продолженной периодическим образом на всю числовую ось берется в форме

(29)

где коэффициенты согласно теоремы о наилучшем приближении есть коэффициенты Фурье-Эйлера

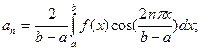
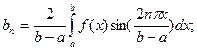(30)

погрешность приближения при этом оценивается по среднеквадратичному

(31)

и по заданному допуску определяется порядок 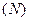тригонометрического полинома.

2.6.2. Применение рядов Фурье-Эйлера при решении краевых задач для обыкновенных дифференциальных уравнений с неоднородной правой чатью-кусочно-непрерывной функцией.

Постановка задачи: найти в классе () раз дифференцируемых непрерывных функций решение краевой задачи для линейного обыкновенного дифференциального уравнения порядка

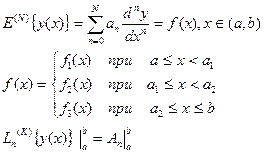(32)

Аппроксимируя правую часть уравнения тригонометрическим рядом Фурье-Эйлера на интервале

(33)

с коэффициентами

(34)

преобобразуем исходную задачу для уравнения с разрывной правой частью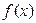

в редуцированную задачу для уравнения с непрерывной правой частью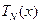

(35)

Разлагая искомое решение на общее решение однородного и частное неоднородного уравнения имеем

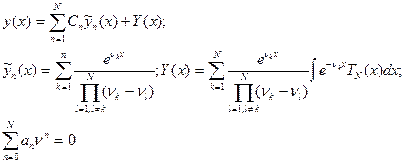(36)

где произвольные постоянные 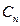интегрирования определяются из граничных условий, а характеристические 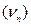числа (показатели) – из соответствующего векового (характеристического уравнения). Здесь приведена формула для частного решения в случае действительных простых (некратных) показателей. Для кратных в указанной формуле следует провести предельный переход, а для комплексно-сопряженных простых (некратных) следует учесть произведения комплексно-сопряженных чисел.

Дата добавления: 2015-07-02