Примеры

Задание № 1. Разложить функцию 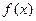в ряд Фурье-Эйлера на интервале 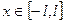, удерживая первые восемь не нулевых слагаемых

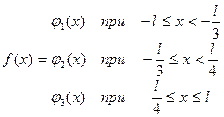
Построить график функции 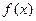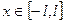. В точках разрыва 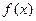указать значения 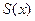ряда Фурье-Эйлера для этой функции. В рассматриваемом варианте

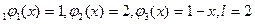
РЕШЕНИЕ. Период функции 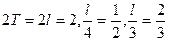. Используя формулы для коэффициентов Ф-Э, имеем

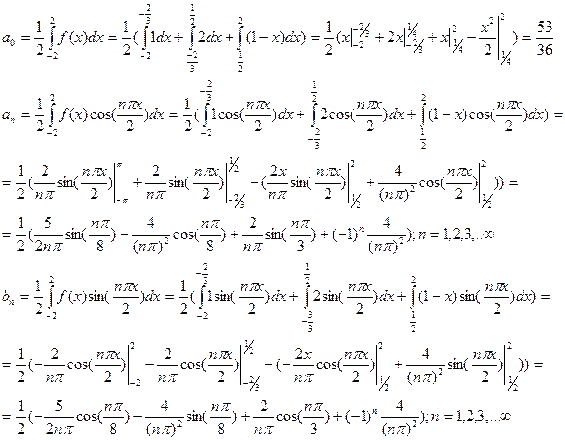
В точках разрыва значения сумм ряда соответственно равны

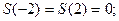
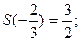
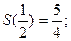
Задание № 2. С помощью ряда Фурье-Эйлера найти решение краевой задачи для обыкновенного дифференциального уравнения четвертого порядка (изгиба однородной балки постоянного поперечного сечения из линейно упругого материала)

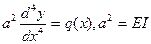
где: 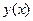- прогиб срединной линии балки; 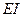- момент инерции прямоугольного сечения балки относительно оси перпендикулятной плоскости изгиба; при граничных (краевых условиях) соответствующих схеме, указанной в таблице № 1. Функция 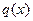, 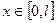в правой части уравнения кусочно-непрерывная и ограничена на интервале

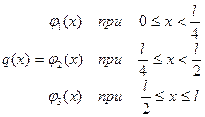
Схема краевой задачи приведена на таблице № 2. Вычислить, учитывая первые восемь отличных от нуля члена ряда, значения функции и при 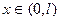. В рассматриваемом варианте (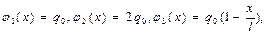), а схема закрепления I (шарнирное закрепление)- равны нулю прогибы 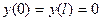и изгибающие моменты 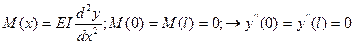конечных точек.

РЕШЕНИЕ. Представляя кусочно-непрерывную правую часть уравнения (нагрузку) непрерывной с помощью разложения Фурье-Эйлера по синусам

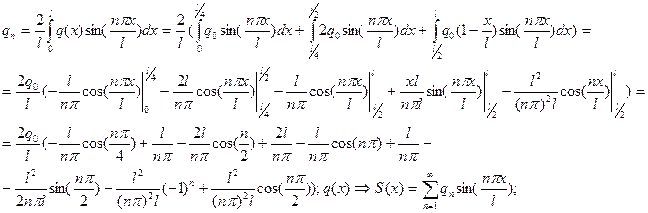
после интегрирования получим

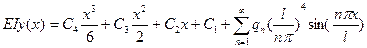
После подстановки в краевые условия получаем

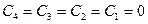
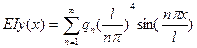
и значение прогиба в середине пролета будет

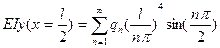
Литература.

1. Кудрявцев В.А., Демидович Б.П., Краткий курс высшей математики. -М.: Наука, 1986. -576 с.

2. Бугров Я.С., Никольский С.М.. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. –М.: Наука, 1989. –464 с.

3. Ильин В.А., Позняк Э.Г..Основы математического анализа –М.: Наука, 1967. – 571 с.

4. Овчинников П.Ф., Лисицын Б.М., Михайленко В.М.. Высшая математика. –К.: Выща шк., 1989. –679 с.

5. Долгов Н.М.. Высшая математика. –К.: Выща шк., 1988. – 416 с.

6. Романовский П.И.. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. –М.: Наука, Физматгиз. 1973.- 336 с.

7. Будак Б.М., Фомин С.В.. Кратные интегралы и ряды. –М.: Наука, Физматгиз. 1967. – 607 с.

8. Лопаницын Е.А.. Ряды Фурье. (Методические указания). –М.: МАМИ, 1988.-37с.

9. Коган Е.А., Попович В.Е.. Ряды Фурье. Дифференциальные уравнения в частных производных. Теория вероятностей. Ч.2.(Методическое пособие № 1393 (1155)).-М.: МАМИ. 1988. –99с.

10. Коган Е.А., Лопаницын Е.А.. Ряды Фурье. Уравнения математической физики.

(Методическое пособие).-М.: МАМИ. 2004. –89с.

11. Сборник задач по математике для втузов. Ч.1-2. /Болгов В.А., Ефимов А.В., Каракулин А.Ф., Коган С.М., Лунц Г.Л., Поспелов А.С., Фролов С.В., Шостак Р.Я., Янполский А.Р..-М.: Наука, Физматгиз, 1986. –426 с.,– 368с.

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА по разделу РЯДЫ ФУРЬЕ-ЭЙЛЕРА

Задание № 1. Разложить функцию 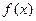в ряд Фурье-Эйлера на интервале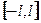

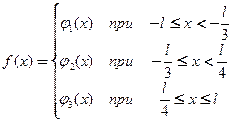
Значения 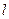и выражения 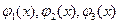приведены в таблице № 1.1. Построить график функции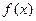 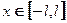. В точках разрыва указать значения суммы 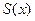ряда Фурье-Эйлера для этой функции.

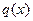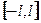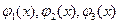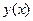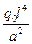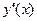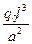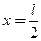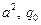Задание № 2. С помощью ряда Фурье найти решение краевой задачи, формулировка которой приведена в таблице № 1.2. Функция в правой части уравнения кусочно непрерывная м ограниченная на интервале . Схему краевой задачи и выражения функций взять из таблицы № 1.3. Вычислить три отличных от нуля члена ряда, значения функции в величинах и в величинах при : и 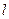– константы

Рапределение составляющих 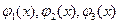нагрузки 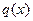по длине балки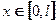

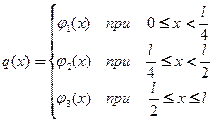
Таблица № 1.2. Краевые условия для различных схем (номеров I,II и III)

Таблица № 1.1. Значения составляющих 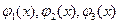функции

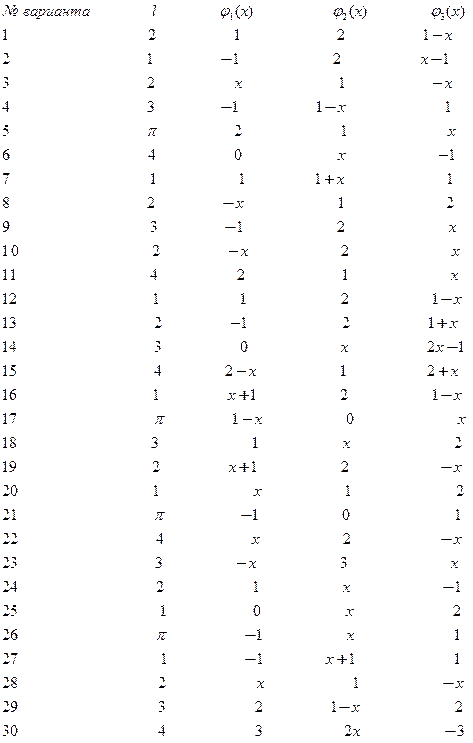
Таблица № 1.3. Схемы (номера I,II и III), составляющие нагрузки .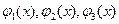

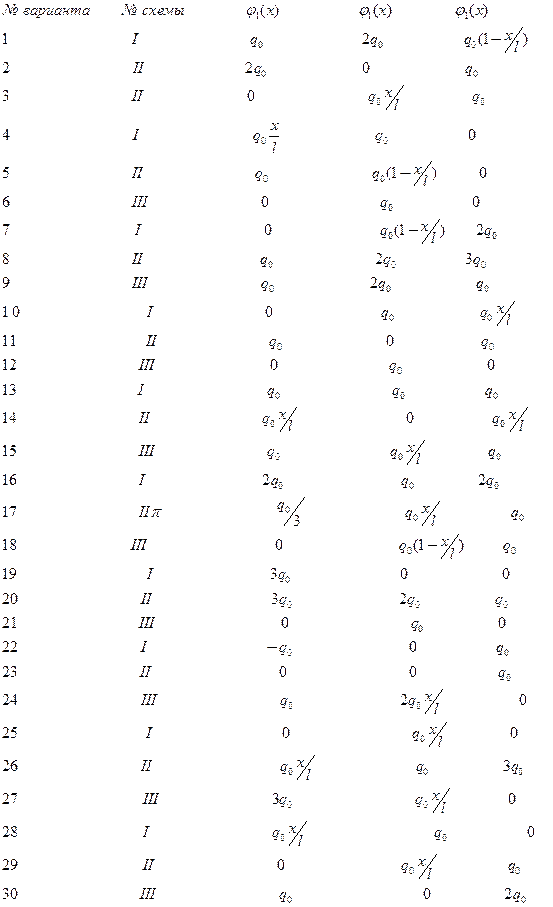
Дата добавления: 2015-07-02