
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритмы управления движущимся объектом
|
|
|
|
Методика решения дифференциальных уравнений движения
Дифференциальные уравнения движения
Дифференциальные уравнения
Из курса физики известно, что движение объектов может быть упрощенно описано дифференциальными уравнениями первого порядка:
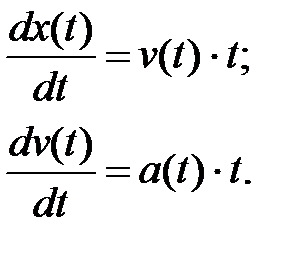
где x (t) – путь, пройденный объектом;
v (t) - скорость объекта;
a (t) – ускорение объекта;
t – время.
Самый простой способ решения дифференциальных уравнений в приращениях – метод Эйлера 1-го порядка:
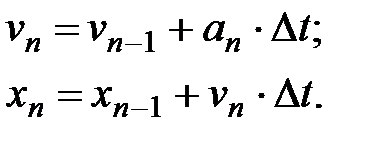
где an – текущее значение ускорения;
vn – текущее значение скорости;
vn -1 – предыдущее значение скорости, рассчитанное на предыдущем шаге расчета;
xn – текущее значение пути;
xn -1 – предыдущее значение пути, рассчитанное на предыдущем шаге расчета;
∆t - шаг расчета по времени.
Дифференциальные уравнения необходимо решать каждый раз, когда рассчитывается новое положение объектов, то есть в обработчике события таймера. Шагом же расчета по времени ∆ t будет являться значение свойства таймера «Interval».
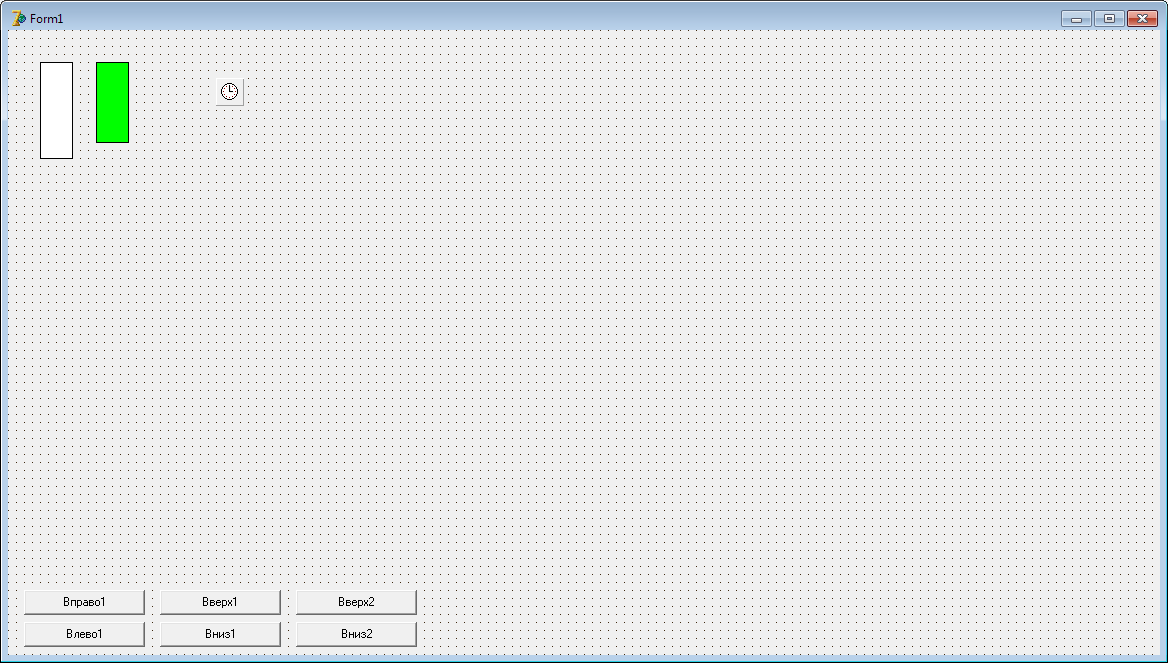
В качестве примера решим задачу, поставленную в п. 2.1.3. На форму Form1 необходимо поместить объекты Shape1 и Shape2, таймер Timer1 и 6 кнопок управления механизмами. Вид получившейся формы представлен на рисунке 2.4. Размеры Shape1 и Shape2 не имеют значения, так как в программе будет произведено их масштабирование.
Свойство Timer.Enabled необходимо выставить равным True, а свойство Form1.BorderStyle, равным bsSingle для предотвращения изменения размера формы самим пользователем.
| Shape1 |
| Shape2 |
| Timer1 |
| Button1 |
| Button2 |
| Button3 |
| Button4 |
| Button5 |
| Button6 |
Рисунок 2.4 – Вид формы
Для того, чтобы решить задачу, поставленную в п. 2.1.3, необходимо организовать две математические модели для каждого механизма в отдельности. Параметры этих моделей организуем в записи (структуры). На языке Pascal:
type TMeh1 = record
Nx: shortint; // задание направления движения по оси x
// (-1 - влево, 0 - стоп,+1 - вправо)
Ny: shortint; // задание направления движения по оси y
// (-1 – вверх, 0 - стоп,+1 - вниз)
vx: real; // скорость по оси x
vy: real; // скорость по оси y
x1: real; // положение по оси x
y1: real; // положение по оси y
end;
type TMeh2 = record
Ny: shortint; // задание направления движения по оси y
// (-1 – вверх, 0 - стоп,+1 - вниз)
vy: real; // скорость по оси y
y2: real; // положение по оси y
end;
Две глобальные переменные типа TMeh1 и TMeh2 будут являться математическими моделями механизма 1 и 2 соответственно:
var
Meh1: TMeh1;
Meh2: TMeh2;
D: real;
LeftMin, TopMin:integer;
Глобальная переменная D будет хранить итоговый масштаб пересчета метров в пиксели (2.2). Переменные LeftMin и LeftMax определяют минимальные расстояния до объекта Shape1, отображающее поведение механизма 1 (формула 2.3).
Ускорения, максимальные перемещения механизмов, максимальные скорости перемещения и геометрические размеры механизмов зададим в виде констант:
const
L = 10; // перемещение по горизонтали механизма 1, м
H = 5; // перемещение по горизонтали механизма 1, м
d1 = 1; // горизонтальный размер механизма 1, м
d2 = 0.7; // горизонтальный размер механизма 2, м
h1 = 3; // вертикальный размер механизма 1, м
h2 = 1; // вертикальный размер механизма 2, м
a1max = 1.5; // ускорение перемещения механизма 1, м/с2
a2max = 4; // ускорение перемещения механизма 2, м/с2
v1ust = 1; // установившаяся скорость механизма 1, м/с
v2ust = 0.6; // установившаяся скорость механизма 2, м/с
Начальные условия прописываются в обработчике событий «OnCreate» формы. Там же происходит вычисление масштаба D и определение размеров объектов Shape1 и Shape2.
procedure TForm1.FormCreate(Sender: TObject);
var
Xmax, Ymax, Dx, Dy: real;
begin
// начальные условия механизма 1
Meh1.Nx:=0;
Meh1.Ny:=0;
Meh1.vx:=0;
Meh1.vy:=0;
Meh1.x1:=0;
Meh1.y1:=0;
// начальные условия механизма 2
Meh2.Ny:=0;
Meh2.vy:=0;
Meh2.y2:=0;
// Вычисление масштаба отображения
Xmax:=L+d1+d2;
Ymax:=H+h1;
Dx:=(90-10)/100*Form1.ClientWidth/Xmax;
Dy:=(70-10)/100*Form1.ClientHeight/Ymax;
if (Dy>Dx) then
begin
D:=Dx;
end
else
begin
D:=Dy;
end;
// изменение размеров Shape
Shape1.Width:=round(D*d1);
Shape1.Height:=round(D*h1);
Shape2.Width:=round(D*d2);
Shape2.Height:=round(D*h2);
// Определение левой и верхней границы перемещения
LeftMin:=round(10/100*Form1.ClientWidth);
TopMin:=round(10/100*Form1.ClientHeight);
// отображение объектов Shape на форме
Risovanie();
end;
Необходимо отметить, что для вычисления некоторых параметров объектов Shape и переменных LeftMin и TopMin целого типа применяется встроенная функция round(), которое округляет десятичные дроби до целого значения.
Для отображения Shape на форме согласно математическим моделям определим пользовательскую процедуру Risovanie, которая вычисляет формулы (2.3) и (2.4). Саму процедуру необходимо поместить впереди обработчика события Form1.OnCreate. Вызов же самой функции помещается в конце обработчика данного события (см. листинг выше).
procedure Risovanie();
begin
Form1.Shape1.Left:=round(D*Meh1.x1+LeftMin);
Form1.Shape1.Top:=round(D*Meh1.y1+TopMin);
Form1.Shape2.Left:=round(D*(Meh1.x1+d1)+LeftMin);
Form1.Shape2.Top:=round(D*(Meh1.y1+Meh2.y2)+TopMin);
end;
Для моделирования перемещения механизмов только при нажатии соответствующих кнопок, используем событие «OnMouseDown» для обработки именно нажатия кнопки, и событие «OnMouseUp» для обработки отпускания кнопки. В первом типе обработчиков необходимо задать направление движения (переменные Meh1.Nx, Meh1.Ny, Meh2.Ny), а во вторых событиях обнулить управляющие переменные. Листинг обработчиков этих событий показан ниже:
procedure TForm1.Button1MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Nx:=+1; // движение механизма 1 вправо
end;
procedure TForm1.Button2MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Nx:=-1; // движение механизма 1 влево
end;
procedure TForm1.Button3MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Ny:=-1; // движение механизма 1 вверх
end;
procedure TForm1.Button4MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Ny:=+1; // движение механизма 1 вниз
end;
procedure TForm1.Button5MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh2.Ny:=-1; // движение механизма 2 вверх
end;
procedure TForm1.Button6MouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh2.Ny:=+1; // движение механизма 2 вниз
end;
procedure TForm1.Button1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Nx:=0; // остановка механизма 1
end;
procedure TForm1.Button2MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Nx:=0; // остановка механизма 1
end;
procedure TForm1.Button3MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Ny:=0; // остановка механизма 1
end;
procedure TForm1.Button4MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh1.Ny:=0; // остановка механизма 1
end;
procedure TForm1.Button5MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh2.Ny:=0; // остановка механизма 2
end;
procedure TForm1.Button6MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
Meh2.Ny:=0; // остановка механизма 2
end;
В обработчике события «OnTimer» объекта Timer1 необходимо реализовать алгоритм движения механизмов с учетом ускорения, замедления, ограничения максимальных перемещений и управляющих переменных.
Диаграмма движения механизма 1 по оси x представлена на рисунке 2.5. При нажатии на кнопку управляющая переменная Nx выставляется равным +1. После этого ускорение принимается равное a1max. Начинается равноускоренное движение с возрастающей скоростью. При достижении скорости значения v1ust, ускорение принимается равное 0 и механизм 1 движется с постоянной скоростью. После отпускания кнопки переменная Nx становится равной 0, знак ускорения принимается обратным знаку скорости. В последствии скорость уменьшается до значения, близкого к нулю и механизм останавливается. Алгоритм программы движения по оси x приведен на рисунке 2.6.
| Нажатие кнопки |
| Отпускание кнопки |
| Meh1.Nx = +1 |
| Meh1.Nx = 0 |
| a = +a1max |
| a = 0 |
| a = -a1max |
| v = +v1ust |
| t |
| Начало |
| Meh1.Nx = 0 |
| да |
| нет |
| Кнопка нажата |
| Meh1.Nx = +1 |
| да |
| нет |
| вправо |
| влево |
| a:= +a1max |
| a:= -a1max |
| Meh1.vx >= v1ust |
| нет |
| да |
| a:= 0 |
| Meh1.vx <= -v1ust |
| нет |
| да |
| a:= 0 |
| Ограничение скорости |
| нет |
| да |
| a:= 0 Meh1.vx:=0 |
| Ограничение положения слева и справа с учетом заданного направления |
| Кнопка отпущена |
| на след. стр. |
| ((Meh1.x1>=L) and (Meh1.Nx>=0)) or ((Meh1.x1<=0) and (Meh1.Nx<=0)) |
| Meh1.vx:=Meh1.vx + a∙∆t Meh1.x1:=Meh1.x1 + Meh1.vx ∙∆t |
| Решение дифференциальных уравнений |
| Алгоритм движения механизма 1 по оси y |
| Алгоритм движения механизма 2 по оси y |
| Risovanie(); |
| Изменение положения Shape на форме |
| Конец |
| Ветка алгоритма, когда кнопка отпущена |
| Meh1.vx > 0 |
| да |
| нет |
| вправо |
| влево |
| a:= -a1max |
| a:= +a1max |
| Meh1.vx <= 0.01×v1ust |
| нет |
| да |
| a:= 0 Meh1.vx:=0 |
| Meh1.vx >= -0.01×v1ust |
| нет |
| да |
| a:= 0 Meh1.vx:=0 |
Рисунок 2.6 – Алгоритм управления движением
Алгоритм движения по другим осям будет аналогичным с учетом ограничений движения механизма 1 по оси y 0<Meh1.y1<H и механизма 2 по оси y 0<Meh2.y2<h1.
Алгоритм, приведенный на рисунке 2.6, достаточно сложный для реализации в программе вследствие многочисленных ветвлений. Для того, чтобы не запутаться при реализации программы необходимо правильно устанавливать отступы, показывая вложения команд, и не забывать сразу прописывать обе ветки ветвления. Для примера приведена последовательность написания программы для блоков 1-9 (рисунок 2.6).
1. Установка шаблона обработчика события «OnTimer». Выбрать объект «Timer1» на форме. В инспекторе объектов выбрать вкладку «Events». Два раза кликнуть левой кнопкой мыши на строчку «OnTimer»:
procedure TForm1.Timer1Timer(Sender: TObject);
begin
end;
2. Объявление локальной переменной «a»:
procedure TForm1.Timer1Timer(Sender: TObject);
var
a:real;
begin
end;
3. Блок сравнения 1 (рисунок 2.6). Сразу необходимо прописать заготовки двух веток «begin-end» через else. Одинаковыми отступами показываем, что обе ветки имеют одинаковую вложенность.
procedure TForm1.Timer1Timer(Sender: TObject);
var
a:real;
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
end
else
begin // кнопка нажата
end;
end;
4. Блок сравнения 2 реализуется в ветке, когда кнопка нажата. Отступом показываем, что этот блок вложен в предыдущий.
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
end
else
begin // кнопка нажата
if Meh1.Nx=+1 then
begin // да
end
else
begin // нет
end;
end;
end;
6. Блок вычисления ускорения 3, блок сравнения 4 и блок обнуления ускорения 5:
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
end
else
begin // кнопка нажата
if Meh1.Nx=+1 then
begin // да
end
else
begin // нет
a:=-a1max;
if Meh1.vx<=-v1ust then
begin // да
a:=0;
end; { // пустую ветку else можно не писать
else
begin // нет
end; }
end;
end;
end;
7. Блок вычисления ускорения 6, блок сравнения 7 и блок обнуления ускорения 8:
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
end
else
begin // кнопка нажата
if Meh1.Nx=+1 then
begin // да
a:=+a1max;
if Meh1.vx>=v1ust then
begin // да
a:=0;
end;
end
else
begin // нет
a:=-a1max;
if Meh1.vx<=-v1ust then
begin // да
a:=0;
end; { // пустую ветку else можно не писать
else
begin // нет
end; }
end;
end;
end;
Аналогично оформляем остальные ветки алгоритма. Для движения по оси x программа будет выглядеть следующим образом:
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
if Meh1.vx>0 then
begin // да вправо
a:=-a1max;
if Meh1.vx<=0.01*v1ust then
begin // да
a:=0;
Meh1.vx:=0;
end;
end
else
begin // нет влево
a:=+a1max;
if Meh1.vx>=-0.01*v1ust then
begin // да
a:=0;
Meh1.vx:=0;
end;
end;
end
else
begin // кнопка нажата
if Meh1.Nx=+1 then
begin // да
a:=+a1max;
if Meh1.vx>=v1ust then
begin // да
a:=0;
end;
end
else
begin // нет
a:=-a1max;
if Meh1.vx<=-v1ust then
begin // да
a:=0;
end; { // пустую ветку else можно не писать
else
begin // нет
end; }
end;
end;
// ограничение положения слева и справа
if ((Meh1.x1>=L) and (Meh1.Nx>=0)) or ((Meh1.x1<=0) and (Meh1.Nx<=0)) then
begin // да
a:=0;
Meh1.vx:=0;
end;
// решение дифф. уравнений по оси x механизма 1
Meh1.vx:=Meh1.vx + a*0.01;
Meh1.x1:=Meh1.x1 + Meh1.vx*0.01;
// Изменение положения Shape на форме
Risovanie();
end;
Можно запустить программу и убедиться в работоспособности перемещения механизма 1 влево и вправо с ускорением.
Полный листинг обработчика события «OnTimer» с обработкой всех перемещений:
procedure TForm1.Timer1Timer(Sender: TObject);
var
a:real;
begin
if Meh1.Nx=0 then
begin // кнопка отпущена
if Meh1.vx>0 then
begin // да вправо
a:=-a1max;
if Meh1.vx<=0.01*v1ust then
begin // да
a:=0;
Meh1.vx:=0;
end;
end
else
begin // нет влево
a:=+a1max;
if Meh1.vx>=-0.01*v1ust then
begin // да
a:=0;
Meh1.vx:=0;
end;
end;
end
else
begin // кнопка нажата
if Meh1.Nx=+1 then
begin // да
a:=+a1max;
if Meh1.vx>=v1ust then
begin // да
a:=0;
end;
end
else
begin // нет
a:=-a1max;
if Meh1.vx<=-v1ust then
begin // да
a:=0;
end; { // пустую ветку else можно не писать
else
begin // нет
end; }
end;
end;
// ограничение положения слева и справа
if ((Meh1.x1>=L) and (Meh1.Nx>=0)) or ((Meh1.x1<=0) and (Meh1.Nx<=0)) then
begin // да
a:=0;
Meh1.vx:=0;
end;
// решениe дифф. уравнений по оси x механизма 1
Meh1.vx:=Meh1.vx + a*0.01;
Meh1.x1:=Meh1.x1 + Meh1.vx*0.01;
// -------------------- Механизм 1 по оси y -----------------------------------
if Meh1.Ny=0 then
begin // кнопка отпущена
if Meh1.vy>0 then
begin // да
a:=-a1max;
if Meh1.vy<=0.01*v1ust then
begin // да
a:=0;
Meh1.vy:=0;
end;
end
else
begin // нет
a:=+a1max;
if Meh1.vy>=-0.01*v1ust then
begin // да
a:=0;
Meh1.vy:=0;
end;
end;
end
else
begin // кнопка нажата
if Meh1.Ny=+1 then
begin // да
a:=+a1max;
if Meh1.vy>=v1ust then
begin // да
a:=0;
end;
end
else
begin // нет
a:=-a1max;
if Meh1.vy<=-v1ust then
begin // да
a:=0;
end;
end;
end;
// ограничение положения слева и справа
if ((Meh1.y1>=H) and (Meh1.Ny>=0)) or ((Meh1.y1<=0) and (Meh1.Ny<=0)) then
begin // да
a:=0;
Meh1.vy:=0;
end;
// решениe дифф. уравнений по оси y механизма 1
Meh1.vy:=Meh1.vy + a*0.01;
Meh1.y1:=Meh1.y1 + Meh1.vy*0.01;
// -------------------- Механизм 2 по оси y -----------------------------------
if Meh2.Ny=0 then
begin // кнопка отпущена
if Meh2.vy>0 then
begin // да
a:=-a2max;
if Meh2.vy<=0.01*v2ust then
begin // да
a:=0;
Meh2.vy:=0;
end;
end
else
begin // нет
a:=+a2max;
if Meh2.vy>=-0.01*v2ust then
begin // да
a:=0;
Meh2.vy:=0;
end;
end;
end
else
begin // кнопка нажата
if Meh2.Ny=+1 then
begin // да
a:=+a2max;
if Meh2.vy>=v2ust then
begin // да
a:=0;
end;
end
else
begin // нет
a:=-a2max;
if Meh2.vy<=-v2ust then
begin // да
a:=0;
end;
end;
end;
// ограничение положения слева и справа
if ((Meh2.y2>=(h1-h2)) and (Meh2.Ny>=0)) or ((Meh2.y2<=0) and (Meh2.Ny<=0)) then
begin // да
a:=0;
Meh2.vy:=0;
end;
// решениe дифф. уравнений по оси y механизма 1
Meh2.vy:=Meh2.vy + a*0.01;
Meh2.y2:=Meh2.y2 + Meh2.vy*0.01;
// Изменение положения Shape на форме
Risovanie();
end;
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!