Основные принципы расчета и проектирования трубопроводов

В зависимости от величины потерь напора все трубопроводы подразделяют на гидравлически короткие и гидравлически длин­ные, причем их проектирование и расчет имеют существенные различия.

Короткими считают трубопроводы небольшой длины, имеющие, как правило, большое количество местных сопротивлений, в кото­рых местные потери составляют примерно 5—10% потерь напора на трение по длине. В длинных трубопроводах, наоборот, потери напора на местные сопротивления настолько малы по сравнению с потерями по длине, что их либо не учитывают, либо принимают по эквивалентной длине.

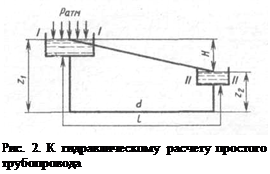
Проектирование длинных трубопроводов начинают с прове­дения топографических изысканий на местности, в результате ко­торых наносят трассу, строят продольный профиль трубопровода, наносят его длину и все высотные отметки (рис. 2).

Расход жидкости и напоры в конечных пунктах обычно за­даны. Чаще всего необходимо определить диаметр трубопровода и напор в его начальном пункте.

При гидравлическом расчете трубопроводов используют уже известные нам основные расчетные зависимости: уравнение Бернулли, уравнение постоянства расхода, уравнение Дарси-Вейсбаха, которое можно преобразовать в одно из следующих выра­жений:

уравнение Шези

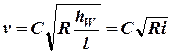, (1)

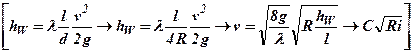
R – гидравлический радиус, 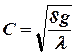– коэффициент Шези.

уравнение расхода жид­кости:

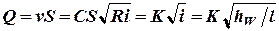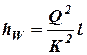или , (2)

где К — расходная характе­ристика трубопровода:

.

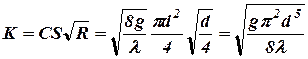Значения расходных ха­рактеристик, вычисленных по этой формуле для всех видов труб, выпускаемых промышленностью, сведены в специальные таблицы, называемые таблицами Шевелева. В упрощенных расчетах для создания запаса в размерах диа­метров труб, необходимого для преодоления местных сопротивлений, в уравнение для определения потерь часто вводят коэф­фициент, увеличивающий расчетные потери напора по длине на 5-10%. При этом, чем длиннее трубопровод, тем меньше процент запаса. Например, с учетом десятипроцентного запаса уравнение потерь примет вид (из (2)):

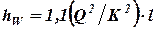. (3)

Вводя понятие располагаемого напора и объединив все потери, получим другой вид расчетного уравнения Бернулли:

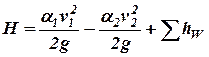, (4)

где 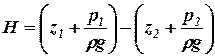- располагаемый напор трубопровода; 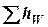- суммарные потери напора в трубопроводе.

Если площади сечений питателя и приемника достаточно велики по сравнению с сечением трубопровода (например, при подаче воды из водоема в резервуар), то скоростными напорами в этих сечениях пренебрегают, и тогда уравнение (4) еще больше упро­щается:

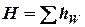. (5)

Уравнение (5) показывает, что весь располагаемый напор тратится на преодоление гидравлических сопротивлений. Это уравне­ние применимо независимо от размеров питателя и приемни­ка, если трубопровод имеет большую длину, а скоростные напоры на входе и выходе оказываются пренебрежительно малыми по сравнению с потерями напора на трение по его длине.

При этом могут иметь место два случая: истечение жидкости под уровень и в атмосферу. При истечении под уровень уравнение Бернулли приводится к виду:

,

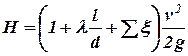а при истечении в атмосферу:

.

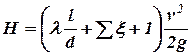Сравнивая эти два уравнения, видим, что они тождественны. Однако необходимо помнить, что при истечении под уровень еди­ница, стоящая в скобках, представляет собой коэффициент местных потерь на выходе потока под уровень, а в случае истечения в ат­мосферу она учитывает кинетическую энергию, оставшуюся в пото­ке при выходе из трубопровода, и представляет собой значение коэффициента Кориолиса при турбулентном режиме: a = 1.

Таким образом, для простого трубопровода длиной l и постоянным диаметром d при турбулентном режиме уравнение Бернулли прини­мает вид:

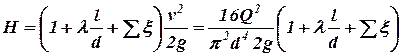. (6)

Коэффициенты сопротивления трения l и местных сопротивле­ний x выбирают, исходя из зависимостей, рассмотренных при изучении гидравлических сопротивлений. При этом могут быть использованы значения коэффициентов, полу­ченные аналитическим, графическим способами или на основе таб­личных данных.

Подставив в формулу (6) значения постоянных величин и вы­числив числовой множитель, получим новый вид расчетного уравне­ния:

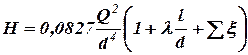. (7)

Дата добавления: 2015-06-27