Расчет простого трубопровода переменного диаметра

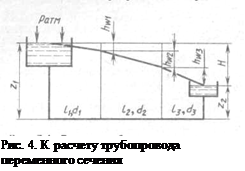
Рассмотрим трубопровод, состоящий из последовательно уло­женных в одну линию труб разных диаметров (рис. 4). Трубопро­вод состоит из трех участков длиной l₁, l₂, l₃ с диаметрами труб, соответственно равными d₁, d₂, d₃.

Уравнение Бернулли для данного случая можно записать в виде:

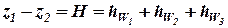, (13)

где 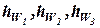- потери напора на первом, втором и третьем участках.

Метод А. Потери напора на первом участке будут равны:

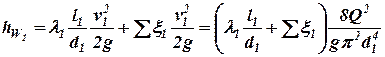. (14)

Аналогично можно выразить потери напора на остальных участках. Подставив выражения для определения потерь на каждом участке в уравнение (13) и просуммировав их, получим

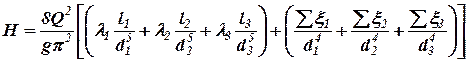. (15)

Метод В. Потери на любом участке можно определить, ис­пользуя также выражения (глава 5):

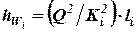. (16)

Тогда:

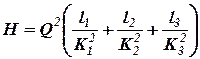. (17)

Или

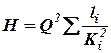(18)

Таким образом, при последовательном соединении труб раз­ных диаметров необходимо суммировать потери на его отдельных участках.

Уравнения (15) и (18) показывают, что решения первой и второй задач для трубопровода переменного сечения будут такими же для трубопровода постоянного сечения.

Третья задача, если в ней требуется определить каждый диа­метр, становится неопределенной, так как каждое уравнение содер­жит число неизвестных, равное числу участков. Чтобы решить эту задачу, нужно задать диаметры труб для всех участков, кроме одного, или использовать графический метод решения.

Обозначив в уравнении (18) 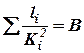, получим упрощенное расчетное уравнение:

H = BQ² (19)

где В - коэффициент, характеризующий величину гидравлических сопротивлений трубопровода, называемый характеристическим коэф­фициентом.

Согласно уравнению (19) потери напора для данного трубо­провода являются только функцией расхода жидкости: H = f(Q).

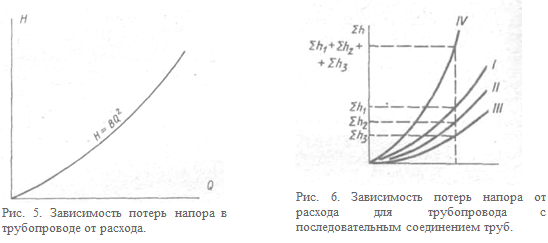
Изобразим эту функциональную зависимость графически. Произ­вольно задаваясь рядом зна­чений расхода, по формуле (19) можно вычислить соответст­вующие им значения потерь напора и, отложив их в масш­табе на координатных осях, по­строить график (рис. 5). По­строенная зависимость имеет вид параболы. Она называется гидравлической характеристикой трубопровода.

Построение гидравлических характеристик позволяет, не при­бегая к расчету, определять потери напора при любом расходе жидкости в рассматриваемом интервале значений Н и Q.

В случае последовательного соединения труб разного диаметра предварительно вычисляют по формуле (19) характеристический коэффициент для каждого участка трубопровода, а затем строят гидравлические характеристики (рис. 6). Кривая I пред­ставляет собой характеристику участка с диаметром d₁ трубопро­вода, кривая II для участка с диаметром d₂, кривая III - для участка с диаметром d₃. Так как при последовательном соединении труб потери напора на отдельных участках суммируются, сум­марную гидравлическую характеристику для всего рассматриваемого трубопровода строят путем графического сложения отрезков кривых I, II, III по вертикали; она выразится кривой IV.

Дата добавления: 2015-06-27