Гидравлический расчет простого трубопровода

Гидравлический расчет трубопроводов обычно сводится к опре­делению одной из трех величин при заданных других:

1) напора Н при известных расходе Q жидкости, диаметре d и длине трубопровода l;

2) расхода Q жидкости при известных диаметре d, длине l трубо­провода и напоре Н;

3) диаметра d трубопровода при заданных расходе Q жидкости и напоре Н.

При расчете трубопроводов могут быть использованы два ме­тода:

метод А - полный, учитывающий все сопротивления трубопрово­да;

метод В - сокращенный, с использованием расходных характе­ристик и поправочных коэффициентов на местные сопротивления.

Рассмотрим три варианта расчета простого трубопровода пол­ным и сокращенным методами.

Задача 1. Даны: длина l трубопровода, диаметр d, геодезические отметки в начальном z₁ и конечном z₂ пунктах и расход Q. Требуется определить высоту Н_б водонапорной башни или напор Н_н, создаваемый насосами.

Для полного расчета (метод А) используем уравнение (6):

.

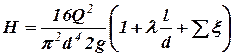Коэффициенты l и x находим с учетом режима движения жидкости, определяемого числом Рейнольдса 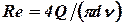, а также в зависимости от шероховатости D труб.

Для сокращения расчета (метод В) используем уравнение (3):

.

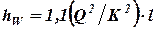Расходная характеристика К определяется из таблиц по заданному диаметру.

Высота башни или напор насоса будут равны:

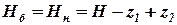. (8)

Задача 2. Даны: длина l трубопровода, диаметр d, высота водонапорной башни Н_б или напор насоса Н_н, геодезические отметки в начальном z₁ и конечном z₂ пунктах. Требуется определить диаметр d трубопровода.

Метод А. Из уравнения (6) находим, что

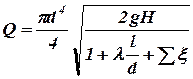. (9)

Прямое вычисление расхода здесь выполнить невозможно, так как коэффициенты l и x являются функциями числа Рейнольдса, а оно оказывается неопределимым в условиях данной задачи потому, что само связано с неизвестным и искомым расходом Q. Поэтому решение производят методом последовательных приближений, полагая в первом приближении, что имеет место квадратичный закон сопротивлений, при котором коэффициенты l и x не зависят от Re.

Метод В. Расчет ведется с использованием уравнения (2):

.

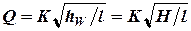Расходная характеристика определяется по таблицам в соответствии с заданным диаметром.

Располагаемый напор Н определяется из соотношения (3):

Н = Н_б + z₁ – z₂.

Расход с учетом 10% запаса на местные потери будет:

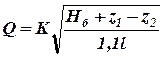. (10)

Задача 3. Даны: высота водонапорной башни Н_б или напор насоса Н_н, расход Q, длина l трубопровода, отметки геодезических высот z₁ и z₂ . Требуется определить диаметр d трубопровода.

Метод А. Решение задачи анали­тическим путем связано со значитель­ными трудностями, так как в этом случае не только неизвестно число Re, куда входит значение диаметра, но и само уравнение (6) или (7) по от­ношению к искомому диаметру ока­зывается уравнением высоких степеней, не приводимых к логарифмическому виду. В связи с этим задачу решают методом последовательного прибли­жения, вначале полагая, что имеет место квадратичный закон сопротивлений, при котором расход Q является функцией диаметра.

Уравнение (9) можно привести к виду:

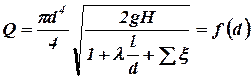. (11)

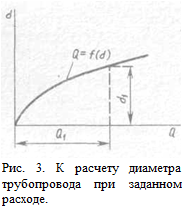
Задаваясь при постоянном напоре Н рядом значений диаметра d₁, d₂, d₃ и т. д., можно вычислить ряд соответствующих значений расхода Q₁, Q₂, Q₃ и т. д. и построить график Q = f(d) (рис. 3). По графику можно определить диаметр трубопровода, отвечающий заданному расходу Q.

Метод В. Имея в виду, что 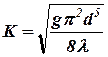, и задаваясь рядом значений d определяем соответствующие им значения расходных характеристик К и строим график, аналогичный графику, показан­ному на рисунке 3.

Вычисляем по формуле 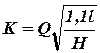расходную характеристику и определяем по графику диаметр. Здесь Н = Н_б + z₁ – z₂.

Можно, используя это же значение К, определить искомый диаметр трубопровода по таблицам Шевелева.

Иногда при решении рассматриваемой задачи вводятся дополни­тельные условия. К таким условиям, в частности, относится полу­чение наинизшей стоимости подачи воды, так как при прочих рав­ных условиях размер диаметра трубы определяет и величину потерь напора. Чем меньше диаметр трубы, тем больше потери напора, и наоборот. Поэтому при проектировании исходят из тре­бований экономической целесообразности, которая зависит от капи­тальных и эксплуатационных затрат.

Меньшие размеры труб требуют меньших капитальных затрат на строительство трубопровода. Стоимость таких труб, затраты на рабо­ты по рытью траншей и укладке труб при этом будут ниже. Однако уменьшение диаметра трубопровода приводит к увеличению потерь напора, что требует большей мощности насосов, электродви­гателей, т. е. большего расхода электроэнергии; следовательно, повышаются стоимость оборудования и затраты на его эксплуатацию.

Определение экономически выгодного диаметра трубопровода обычно имеет компромиссное решение, которое соответствует опти­мальной стоимости капитальных и эксплуатационных затрат. Его определение может быть выполнено графическим или расчетным путем.

Для определения экономически целесообразного диаметра тру­бопровода можно воспользоваться формулой, предложенной В. С. Яблонским. Он установил, что экономически наивыгоднейший диаметр соответствует скоростям течения жидкости, равным пример­но v = 1 м/с, и, решив известное уравнение для расхода жидко­сти относительно диаметра, получил:

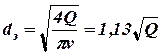(12)

где d_э - диаметр, м; Q - расход жидкости, м³/с.

В машиностроительной гидравлике чаще приходится рассматри­вать гидравлически короткие трубопроводы, например трубопро­воды гидроприводов, системы питания автомобиля или трактора, смазочные системы металлообрабатывающих станков, всасывающие трубопроводы насосов и др. В подобных системах вязкость пере­качиваемой жидкости может намного превосходить вязкость воды. В этих случаях местные потери становятся сопоставимыми с поте­рями напора по длине трубопровода, и ими пренебрегать нельзя.

Принцип расчета гидравлически коротких трубопроводов связан с определением значительного количества коэффициентов местных потерь и их суммированием. Эти расчеты в данном пособии не рассматриваются.

Дата добавления: 2015-06-27