Элементарными преобразованиями

Метод окаймляющих миноров нахождения ранга матрицы

МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

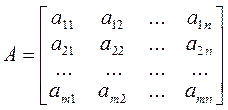
Определение минора.

Минором 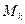порядка k матрицы А называется любой определитель k -го порядка этой матрицы, составленный из элементов, стоящих на пересечении любых её «к» столбцов и любых её «к» строк

		нет
	да
		нет
		нет
	да

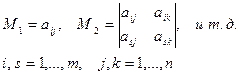
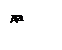
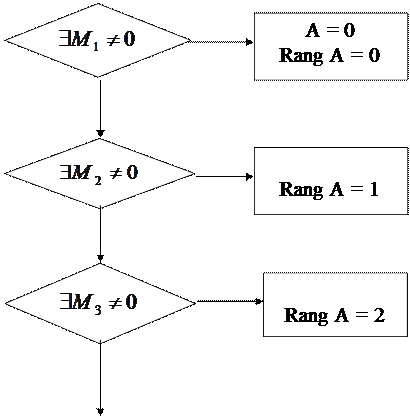Определение ранга матрицы.

Рангом r матрицы А называется наибольший порядок r минора этой матрицы, отличного от нуля: (существует минор порядка r, не равный нулю, а все миноры более высоких порядков равны нулю или не существуют).

Алгоритм приведения матрицы к ступенчатому виду

Условимся называть рабочей строку, которая не изменяется на проводимом этапе элементарных преобразований (перестановке строк; умножении строки на число и сложении с соответствующими элементами другой строки; вычеркиванием всех пропорциональных строк, кроме одной из них).

Рабочая строка первая. Получим нули в первом столбце на местах всех элементов первого столбца за исключением элемента в первой строке а ₁₁. Для этого умножим все элементы первой строки на такие числа, чтобы при сложении с элементами первого столбца остальных строк получить нули в первом столбце, за исключением элемента первой строки а ₁₁.

Если в системе, которую Вы решаете, коэффициент при х ₁ в первом уравнении не равен единице, поменяйте местами строки, записав первой ту, в которой коэффициент при неизвестном х ₁ равен единице.

Если при неизвестном х ₁ во всех уравнениях коэффициенты отличны от единицы, можно:

1) умножить первую строку расширенной матрицы системы на число, противоположное тому, на месте которого Вы хотите получить ноль; а строку, в которой хотите получить ноль, умножьте на коэффициент при х ₁ в первой строке;

2) сложите соответствующие элементы умноженной первой строки и умноженной другой строки.

(3) ~ ~

Далее нужно получить нули во втором столбце ниже главной диагонали.

Рабочая строка вторая. Получаем нули во втором столбце ниже элемента а_{22 .}

Умножим третью строку на (–14) и сложим с соответствующими элементами второй строки. (Или можно было поменять местами вторую и третью строки, чтобы на главной диагонали оказалась единица (см. (*))).

~ ;

(*)

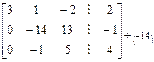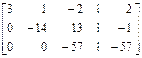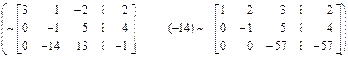Замечание. Полученная в скобках матрица (*) также эквивалентна исходной матрице 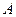, то есть имеет тот же ранг, а системы уравнений, соответствующие этим матрицам, имеют одинаковые решения.

Дата добавления: 2015-06-27