
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
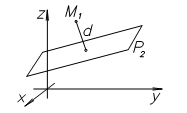
Расстояния d(P1,P2) между плоскостями P1 и P2 и d(L1,L2) между прямыми
|
|
|
|
L 1 и L 2 в R 3, пересечение { P Ç L } плоскости P и прямой L в R 3
ТАБЛИЦА 4
| I P 1 || P 2, L 1 || L 2 в R 3 координатная форма | P 1 || P 2, L 1 || L 2,  векторная форма
векторная форма
| L 1 || L 2 в R 2II координатная форма | |
 Ü
Ü
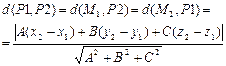

| 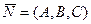 
|  Þ
Þ
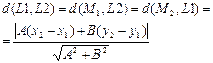 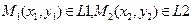
| |
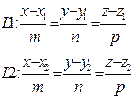 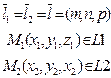
|  
| ||
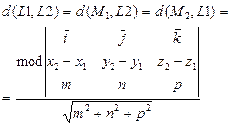 Ü Ü
|  h – высота треугольника h – высота треугольника
| Þ 
| |
| III Прямые L 1 и L 2 скрещиваются в R 3 P 1 || P 2 (L 1Ì P 1, L 2Ì P 2) | Прямая L и плоскость P пересекаются в R 3 IV { P Ç L }= M 1 | ||

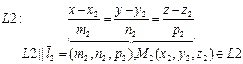
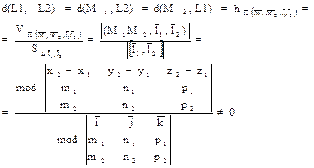 (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота
| 
 M 0(x 0, y 0, z 0) Î L
M 0(x 0, y 0, z 0) Î L
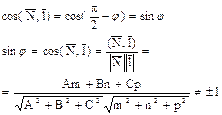 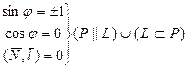 sin j = 0 Û L ^ P, l ïï N
sin j = 0 Û L ^ P, l ïï N
| ||
ТАБЛИЦА 4а (продолжение таблицы 4)
| VI Векторная запись условий ортогональности (P ^ L), коллинеарности (P || L) плоскости P и прямой L в R 3, пересечения P и L (P Ç L). | { P Ç L }= M 1(x 1, y 1, z 1) – координаты точкиV пересечения плоскости P и прямой L в R 3 | |||
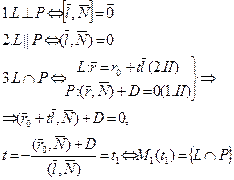
| 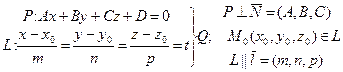  (2.II) Þ (2.II) Þ 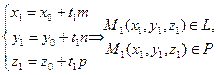
|
к -мерная плоскость Р к в точечно-векторном евклидовом n -мерном пространстве R n
ТАБЛИЦА 5
| к = n – r, Rang A = r | ||||||||||||||
AX = B

| 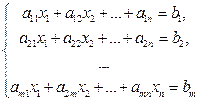
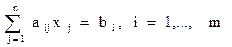
| |||||||||||||
| Система m линейных уравнений с n неизвестными | ||||||||||||||
| r = 1 гиперплоскость к = n –1 | к = 1 прямая в R r+1 n – r = 1 | к-мерная плоскость Р к0 в R n, проходящая через начало координат В =0 (СОЛУ) – система однородных линейных уравнений | Общее решение произвольной системы линейных уравнений В ¹0 (ОРСЛУ) | |||||||||||
| матричная форма | координатная форма | матричная форма | координатная форма | |||||||||||

|

|

| 
|

|
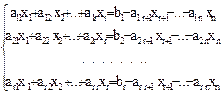
| |||||||||
| Плоскость в R3 n =3 | ||||||||||||||

| 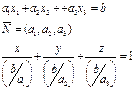 Уравнение плоскости в отрезках;
Уравнение плоскости в отрезках;
| 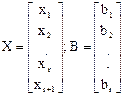 Rang A = r = n –1
n = r + 1
AX=B
Rang A = r = n –1
n = r + 1
AX=B
| AX =0 rang A=r, x1,x2,..,xr – базисные неизвестные. Число базисных неизвестных равно r. | xr+1, xr+2,..,xn – свободные неизвестные Число свободных неизвестных равно k=n – r | Отбросить строки, не вошедшие в базисный минор, перенести свободные неизвестные в правые части уравнений, а дальше следует применить метод Гаусса, Крамера или матричный. | |||||||||
| Прямая в R 3 n =3, r =2, к =1 | Фундаментальная система частных решений СОЛУ (ФСЧР) | Частное решение произвольной СЛУ (ЧРСЛУ) | ||||
форма | координатная форма | Свободным неизвестным придать последовательно значения строк единичной матрицы Е | xr+1 = xr+2 =...= xn = 0 | |||
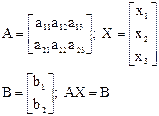
|
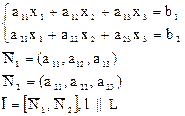
|  АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
|  АС=В
АС=В
| |||
| Прямая в R 2 n = 2, r = 1, k = 1 | Общее решение системы однородных линейных уравнений АХ 0=0 | О. Р. произвольной системы | ||||
| матричная форма | координатная форма | матричная форма | координатная форма | линейных уравнений (ОРСЛУ) АХ=В | ||
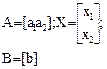 АХ=В АХ=В
|  Уравнение прямых в отрезках
Уравнение прямых в отрезках
| 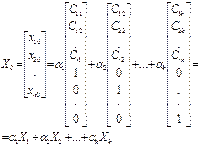
| 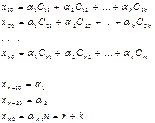
| 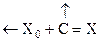 AX=A (X0+C)=
= AX 0+ AC= O+ B=B
AX=A (X0+C)=
= AX 0+ AC= O+ B=B
| ||
 Прямая в Rn=Rr + 1 n = r+ 1, k = 1 Прямая в Rn=Rr + 1 n = r+ 1, k = 1
| ||||||
| координатная форма | матричная форма | |||||
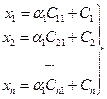 параметрические уравнения,
a 1 – параметр, свободная неизвестная параметрические уравнения,
a 1 – параметр, свободная неизвестная
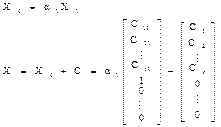
| 
| |||||
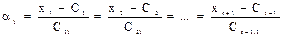 – канонические уравнения – канонические уравнения
| ||||||
| КРИВЫЕ ВТОРОГО ПОРЯДКА | |
| Определение эллипса. | Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек этой плоскости, называемых фокусами эллипса, есть величина постоянная, большая расстояния между фокусами и равная 2a. |
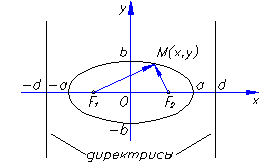 |
a – большая полуось эллипса;
b – малая полуось эллипса;
F1(– с,0) и F2 (с,0) – фокусы эллипса;
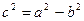 , с – фокусное расстояние эллипса;
, с – фокусное расстояние эллипса;
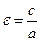 <1,
<1, 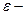 эксцентриситет эллипса;
эксцентриситет эллипса;
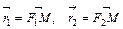 – фокальные радиусы-векторы;
– фокальные радиусы-векторы;
по определению  .
.
Прямые 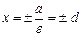 называются директрисами эллипса.
называются директрисами эллипса.
Каноническое уравнение эллипса 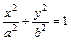 .
.
Строят эллипс, вписывая его в прямоугольник со сторонами длиной 2а и 2b и с центром симметрии в начале координат.
Уравнение эллипса со смещенным при помощи параллельного переноса в точку М0(x0, y0) центром имеет вид
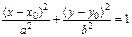 .
.
Чтобы привести общее уравнение эллипса
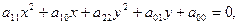 где коэффициенты
где коэффициенты  и
и 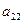
должны иметь одинаковые знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
Например, приведем уравнение кривой
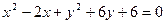
к каноническому виду:

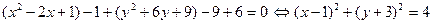 .
.
Полученное уравнение является каноническим уравнением окружности, радиус которой равен 2, а центр находится в точке М (1,–3).
Признак уравнения окружности:
- коэффициенты при квадратах переменных одинаковые;
- отсутствует произведение переменных.
| Определение гиперболы. | Гиперболойназывается множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами и равная 2а. |
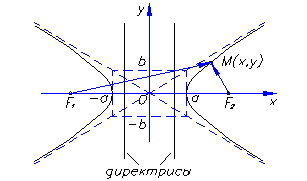 |
a – действительная полуось гиперболы;
b – мнимая полуось гиперболы;
F1(– с,0) и F2 (с,0) – фокусы гиперболы;
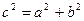 , с – фокусное расстояние гиперболы;
, с – фокусное расстояние гиперболы;
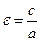 >1,
>1, 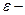 эксцентриситет гиперболы;
эксцентриситет гиперболы;
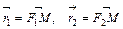 – фокальные радиусы-векторы;
– фокальные радиусы-векторы;
по определению 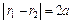 . Прямые
. Прямые 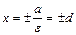 называются директрисами гиперболы. Уравнения асимптот гиперболы имеют вид
называются директрисами гиперболы. Уравнения асимптот гиперболы имеют вид 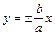 .
.
Каноническое уравнение гиперболы 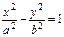 .
.
Строят гиперболу, изобразив предварительно прямоугольник со сторонами длиной 2а и 2b и с центром симметрии в начале координат, а затем вписывают ветви гиперболы в углы между асимптотами гиперболы (прямыми, на которых лежат диагонали прямоугольника), помещая вершины гиперболы в точки с координатами (– а, 0), (а, 0).
Уравнение гиперболы со смещенным при помощи параллельного переноса в точку М0(x0,,y0) центром имеет вид
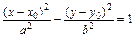 .
.
Чтобы привести общее уравнение гиперболы
 где коэффициенты
где коэффициенты 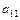 и
и 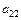 должны иметь противоположные знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
должны иметь противоположные знаки, к каноническому виду, нужно выделить полные квадраты по переменным x и y.
Гипербола, уравнение которой  , называется сопряженной по отношению к гиперболе, имеющей уравнение
, называется сопряженной по отношению к гиперболе, имеющей уравнение  . Фокусы сопряженной гиперболы расположены на мнимой оси.
. Фокусы сопряженной гиперболы расположены на мнимой оси.
| Определение параболы. | Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемойфокусом,и отданной прямой, называемой директрисой и не проходящей через фокус. |

Каноническое уравнение параболы: 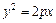 .
.
Строят параболу, откладывая одинаковые отрезки от точек параболы до фокуса с координатами  и до директрисы, уравнение которой
и до директрисы, уравнение которой 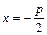 . Вершина параболы находится в точке
. Вершина параболы находится в точке 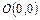 .
.
Уравнение параболы со смещенной при помощи параллельного переноса в точку М0(x0, y0) вершиной имеет вид 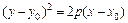 .
.
Чтобы привести общее уравнение параболы  к каноническому виду, нужно выделить полный квадрат по переменной y и удвоенный параметр p по переменной х.
к каноническому виду, нужно выделить полный квадрат по переменной y и удвоенный параметр p по переменной х.
Парабола, уравнение которой 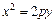 , называется сопряженной по отношению к параболе, имеющей уравнение
, называется сопряженной по отношению к параболе, имеющей уравнение 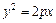 . Фокус сопряженной параболы расположен в точке
. Фокус сопряженной параболы расположен в точке  , а ее директриса имеет уравнение
, а ее директриса имеет уравнение  .
.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 980; Нарушение авторских прав?; Мы поможем в написании вашей работы!
