Сравнение бесконечно малых функций. Пусть (х) и (х) – бесконечно малые функции (б

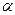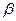Пусть (х) и (х) – бесконечно малые функции (б. м. ф.)

при х 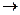а, то есть 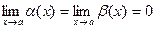, тогда:

1) 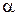(х) – б. м. ф. более высокого порядка малости по сравнению с 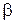(х) – б. м. ф.

при х 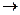а, если

;

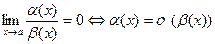2) 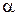(х) – б. м. ф. более низкого порядка малости по сравнению с 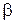(х) – б. м. ф.

при х 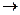а, если

;

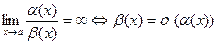3) 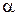(х) и 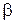(х) – б. м. ф. одинакового порядка малости

при х 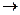а, если

;

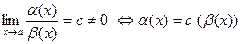4) 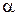(х) и 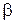(х) – б. м. ф., эквивалентные при х 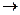а, если

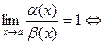a(x)~b(x);

5) 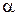(х) – б. м. ф. k -го порядка малости по сравнению с 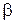(х) –

б. м. ф. при х 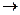а, если

.

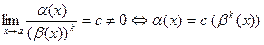Теорема о первом замечательном пределе.

Предел функци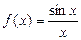и при 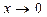существует и равен единице: .

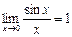Теорема о втором замечательном пределе.

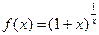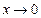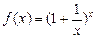Предел функции , если , и функции , если 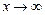, существует и равен числу : .

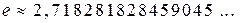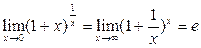Применение первого и второго замечательных пределов позволяет доказать справедливость формул в таблице эквивалентных бесконечно малых функций при х 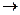а.

	~		~
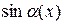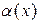
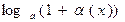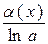
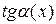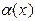
	~	6а	~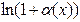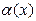
	~		~
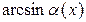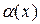
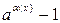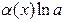
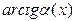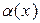
	~	7а	~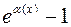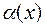
	~		~

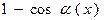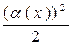
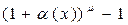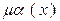
Замечание. В случаях, когда аргумент α(х) функции в вычисляемом пределе стремится не к нулю, а к отличному от нуля числу, например, α(х) 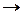а, а 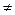0, вводят новую переменную

t = α(х) – а.

Тогда, если α (х) 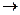а, то t 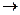0 (функция t (х) должна быть непрерывной функцией в окрестности точки t = 0).

Новая переменная t 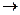0 (при α(х) 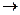а), и для нее легко можно использовать таблицу эквивалентных бесконечно малых функций.

Например, вычислим предел

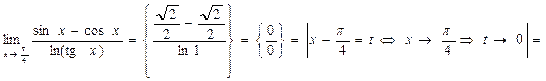Предварительно сделаем следующие преобразования:

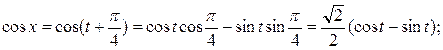
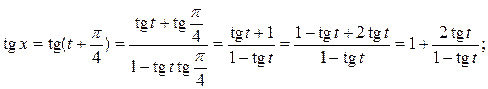
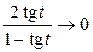при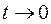

и воспользуемся результатами преобразований:

=

Бесконечно большие функции (б. б. ф.), так же как и бесконечно малые, можно сравнивать между собой.

Если предел отношения двух бесконечно больших функций равен:

1. Бесконечности, тогда в числителе – б. б. ф. более высокого порядка роста;

2. Нулю, тогда в числителе – б. б. ф. более низкого порядка роста;

3. Постоянному числу, не равному нулю или единице, тогда эти бесконечно большие функции одинакового порядка роста;

4. Единице, тогда бесконечно большие функции эквивалентны.

Полезно иметь в виду, что при вычислении пределов отношений конечного числа б. б. ф. складываемых функций слагаемые более низкого порядка роста можно отбрасывать, а сумму заменять слагаемым самого высокого порядка роста.

При 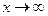самый высокий порядок роста имеет показательная функция 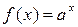; степенная функция 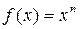имеет порядок роста, более низкий по сравнению с показательной функцией, но более высокий по сравнению с логарифмической; логарифмическая функция 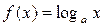имеет самый низкий порядок роста по сравнению и с показательной функцией, и со степенной. Это обозначают так:

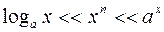, при .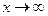

Очень эффективным при вычислении пределов оказывается применение следующих правил:

Дата добавления: 2015-06-27