План интегрирования рациональных дробей

Метод интегрирования по частям

Метод непосредственного интегрирования

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

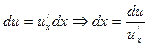
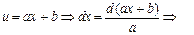
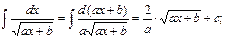
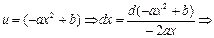
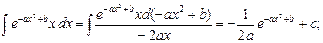
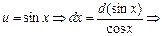
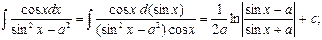
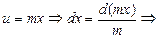
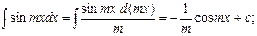
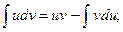
№ п/п	Интеграл	Разбиение подынтегрального выражения на части		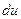v	Результат применения метода
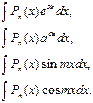
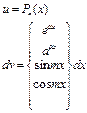
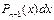
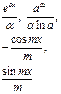
					Метод применяют n раз, пока степень многочлена не понизится до нулевой
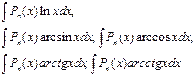
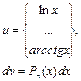
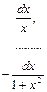
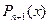
					Получают интеграл от функций степеней х
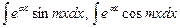
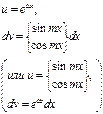
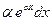
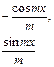
	Циклические интегралы:				Метод применяют 2 раза, получая уравнение относительно искомого интеграла

.

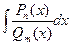Р_n (x) = a ₀x ⁿ + a ₁x ^n-1 + a₂x ^n-2 + …….+ a _{n ,}

Q_m (x)= b₀x^m + b₁x^m-1 + b₂x^m-2 + ……. + b_{m .}

I. 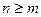– дробь неправильная; 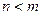– дробь правильная (степень Р_n (x) меньше)

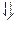(степень n Р_n (x) больше или равна степени m Q_m (x))

Р_n (x) Q_m (x)

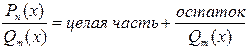
…… целая часть

r_s (x) – остаток (s<m)

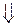
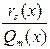– прав. дробь.

II. Знаменатель Q_m (x) разложить на множители линейные – (x-a) и квадратичные – (x²+px+q). Правильную дробь разложить на сумму простых дробей в зависимости от множителей знаменателя.

Вид множителя в знаменателе дроби	Сколько дробей	Сумма простых дробей, соответствующая множителю в знаменателе правильной рациональной дроби
(x-a) ^k	k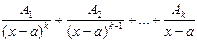
(x^2+px+q) ^w	w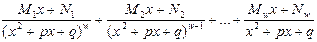

III. Найти неопределенные коэффициенты A, M, N, приведя сумму дробей к общему знаменателю и приравняв числители исходной правильной дроби и суммы дробей.

IV. Проинтегрировать простые дроби:

а) дроби первого типа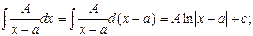

б) дроби второго типа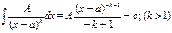

в) дроби третьего типа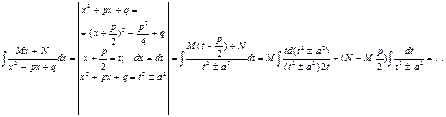

г) дроби четвертого типа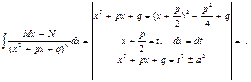

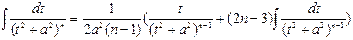– рекуррентная формула

Дата добавления: 2015-06-27