
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследования функции без применения производных
|
|
|
|
Раскрытие неопределенностей по правилу Лопиталя
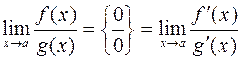

| № п/п | Вид неопределенности | Преобразования | Результат преобразований (c, d – const ≠ 0) |

|

|
 или или 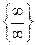 – применить правило Лопиталя – применить правило Лопиталя
| |

| 2.1. дроби привести к общему знаменателю;
2.2. умножить и разделить разность функций на сопряженное выражение, если это разность квадратных корней;
2.3. умножить и разделить разность функций на неполный квадрат суммы этих функций, если это разность корней кубических;
2.4. 
|  ; ;  ; ;
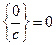 ; ; 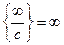 ; ;

 или или 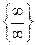 – применить правило Лопиталя – применить правило Лопиталя
| |

| 3.1. 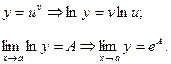 3.2.
3.2. 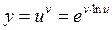
| См. выше |
| № п/п | Цель исследования | Действия | Вывод |
| Найти область определения функции | Найти точки, в которых функция не определена или не задана (точки разрыва графика функции) | Исключить найденные точки из области определения функции | |
| Найти вертикальные асимптоты | Вычислить односторонние пределы функции в точках разрыва и в точках, «подозрительных» на разрыв для кусочно-аналитической функции | Если хотя бы один из односторонних пределов в исследуемой точке равен бесконечности, то график функции имеет вертикальную асимптоту:
 – вертикальная асимптота – вертикальная асимптота
| |
| Исследовать функцию на четность и нечетность | Если 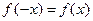 ,
то функция четная.
Если ,
то функция четная.
Если 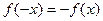 ,
то функция нечетная ,
то функция нечетная
| Ограничиться исследованием функции на интервале 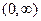 . График четной функции симметричен относительно оси OY, график нечетной функции симметричен относительно начала координат . График четной функции симметричен относительно оси OY, график нечетной функции симметричен относительно начала координат
| |
| Исследовать функцию на периодичность | T – период функции – (наименьшее из всех возможных значений, удовлетворяющих уравнению:
 ) )
| Ограничиться исследованием на интервале, по длине равном периоду T, за пределы интервала продолжить график функции периодическим образом | |
| Найти точки пересечения с осями координат | Решив уравнение  , найти , найти  .
Найти .
Найти 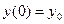
| Точка пересечения графика с осью OX:  .
Точка пересечения графика с осью OY: .
Точка пересечения графика с осью OY: 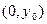
| |
| Найти наклонные, в частности, горизонтальные асимптоты | Вычислить пределы  и и 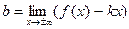
| Если k и b – конечные числа, то уравнение наклонных асимптот 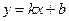 , причем, при , причем, при  асимптота горизонтальная асимптота горизонтальная 
|
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 775; Нарушение авторских прав?; Мы поможем в написании вашей работы!