
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование иррациональностей
|
|
|
|
Интегрирование тригонометрических и гиперболических функций
| № п/п | Подынтегральная функция | Подстановка | Вспомогательные преобразования | Итог |
 рациональная функция относительно
sin x,
cos x рациональная функция относительно
sin x,
cos x
| Универсальная
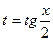
| 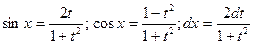
| Подынтегральная функция рациональная относительно х | |
 Нечетная относительно
сos x
Нечетная относительно
сos x
| 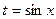
| 
| ||
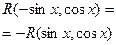 Нечетная относительно
sin x
Нечетная относительно
sin x
| 
| 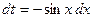
| ||
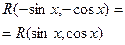 Четная относительно
сos x и sin x
Четная относительно
сos x и sin x
| 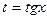
| 
| ||

| 
| |||
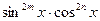 Степени четные неотрицательные
Степени четные неотрицательные
| 
| Понижение степени | ||

| 
| Сумма функций | ||
 Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций
|
| Подынтегральная функция | Подстановка | Итог | ||
 R – рациональная функция,
R – рациональная функция, 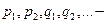 целые числа целые числа
|
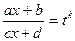 , где , где  ─ наименьшее общее кратное знаменателей показателей: ─ наименьшее общее кратное знаменателей показателей:
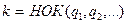
| Рациональная функция 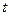
| ||

|

| Рациональная функция 
| ||
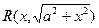

|
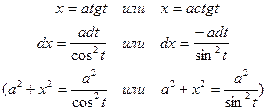
| |||
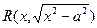
|  
| |||
Дифференциальный бином

| p ─ целое число, m,n ─ дроби |
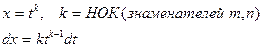
| Рациональная функция 
| |
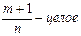
| 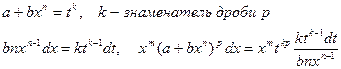
| |||

| 
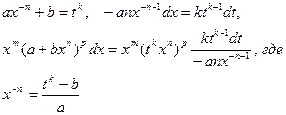
| |||

| 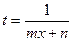
| См. пункт | ||

| 
| Два табл-х инт-ла |
При нахождении первообразной функции можно пользоваться следующим алгоритмом:
- Попытаться применить непосредственное интегрирование;
2. Если это не удается, определить класс функции (рац. дробь, тригонометрическая, иррациональная) и применить соответствующие подстановки, а если функция смешанных классов – интегрирование по частям.
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Теорема. Если величина Q обладает на [ a,b ]
1. свойством аддитивности, а именно, если a = x0 £ x1 £ x2 £…£ xn = b,
то Q=DQ1+DQ2+…+DQn, где D Qi – значение Q на [ xi-1,xi ], i=1,2,…n;
2. свойством линейности Q в малом: D Q» f(x)D x, где f (x) – интегрируемая на [a,b ]функция,
то величину Q можно найти интегралом от ее элемента dQ = f (x) dx по промежутку [ a,b ]:
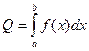
| Q | № | Чертеж | Система координат и пояснения | Формула | Q | ||||||
| S, п л ощ а д ь п л о с к о й ф и г у р ы D | 
| Д. С. К.
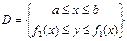 Одна кривая границы области D не выше другой.
Одна кривая границы области D не выше другой.
|

| S, п л о щ а д ь п л о с к о й ф и г у р ы D | |||||||

| Д. С. К.
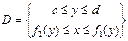 Одна кривая границы области D не левее другой.
Одна кривая границы области D не левее другой.
|
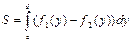
| |||||||||

| Д. С. К. a £ t £ b x (a) =a, x (b) =b (y(t) ³0, " tÎ [a,b ]) Верхняя граница области задана параметрически |

| |||||||||
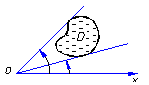 | П. С. К.

|

| |||||||||
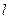 ,
д
л
и
н
а
к
р
и
в
о
й
L ,
д
л
и
н
а
к
р
и
в
о
й
L
| 
| Д. С. К.

|

| 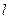 ,
д
л
и
н
а
к
р
и
в
о
й
L ,
д
л
и
н
а
к
р
и
в
о
й
L
| |||||||
Д. С. К.

|
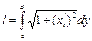
| ||||||||||

| Д. С. К.
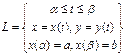 Линия L задана параметрически
Линия L задана параметрически
|

| |||||||||

| П. С. К.
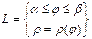
|
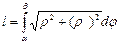
|
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
| Q | № | Чертеж | Система координат и пояснения | Формула | Q |
| V, о б ъ е м т е л а Т | 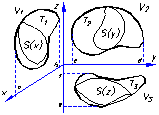
| Д. С. К.

| 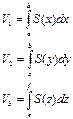
| V, о б ъ е м т е л а Т | |
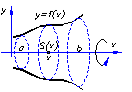
| Д. С. К.
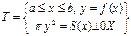 Тело Т образовано вращением кривой у=f (х) вокруг оси 0 Х
Тело Т образовано вращением кривой у=f (х) вокруг оси 0 Х
|

| |||
| s, п л ощ а д ь п о в е р х н. ω |
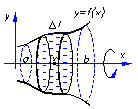
| Д. С. К.
 Поверхность v образована вращением кривой у=f (х) вокруг оси 0 Х
Поверхность v образована вращением кривой у=f (х) вокруг оси 0 Х
|

| s, п л о щ а д ь п о в е р х н. w | |
Д. С. К.
 Поверхность v образована вращением кривой у=f (х (t)), заданной параметрически, вокруг оси 0 Х
Поверхность v образована вращением кривой у=f (х (t)), заданной параметрически, вокруг оси 0 Х
|

| ||||
| S, п у т ь | 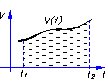
| Д. С. К.
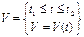 V – скорость прямолинейного движения тела на промежутке времени [ t1,t2 ]
V – скорость прямолинейного движения тела на промежутке времени [ t1,t2 ]
|
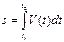
| S, п у т ь | |
| А, р а б о т а | 
| Д. С. К.
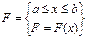 Сила F направлена параллельно оси 0 Х на промежутке [ a,b ]
Сила F направлена параллельно оси 0 Х на промежутке [ a,b ]
|

| А, р а б о т а | |
| Р,д а в л | 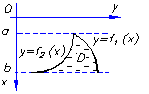
| Д. С. К.
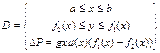 m – плотность жидкости, давящей на пластину D
m – плотность жидкости, давящей на пластину D
|

| Р, д а в л. | |
| m,м а с с а | 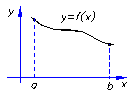
| Д. С. К.
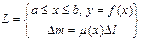 m – линейная плотность кривой L
m – линейная плотность кривой L
|
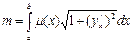
| m,м а с с а |
Статические моменты относительно координатных осей Sx , Sy ,, моменты инерции Мх,, Му, координаты центра тяжести хс, ус плоской кривой
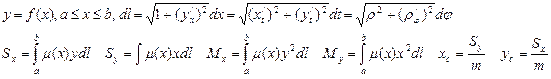
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ФНП)
Определениечастной производной.
Если в точке М (х, у) существует предел отношения частного приращения ФНП z = f (x,y) по одному из ее аргументов к приращению этого аргумента при стремлении приращения аргумента к нулю, то этот предел называется частной производной ФНП по этому аргументу в точке М (х, у):
 ; ;
 .
Правило.Чтобы найти частную производную ФНП по одному из ее аргументов, надо все остальные аргументы ФНП считать постоянными и применять правила дифференцирования и таблицу производных функции одного аргумента, по которому берется частная производная .
Правило.Чтобы найти частную производную ФНП по одному из ее аргументов, надо все остальные аргументы ФНП считать постоянными и применять правила дифференцирования и таблицу производных функции одного аргумента, по которому берется частная производная
| Градиент функции 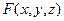 : :
 Градиент функции в точке характеризует направление и величину максимальной скорости возрастания этой функции в данной точке.
Градиент функции в точке характеризует направление и величину максимальной скорости возрастания этой функции в данной точке.
| Экстремум функции двух переменных
1. Необходимое условие существования экстремума.
Если функция f (x,y) имеет в точке М0 (х0,у0) экстремум и имеет в точке М0 частные производные первого порядка, то в этой точке частные производные первого порядка равны нулю, т. е.
 .
2. Достаточные условия существования экстремума.
Пусть .
2. Достаточные условия существования экстремума.
Пусть 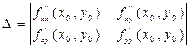 . Тогда
а) если D> 0, то в точке М0 функция имеет экстремум, причем при . Тогда
а) если D> 0, то в точке М0 функция имеет экстремум, причем при 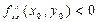 – локальный максимум, при – локальный максимум, при  – локальный минимум;
б) если D<0, то в точке М0 экстремума нет;
в) если D=0, то требуются дополнительные исследования. – локальный минимум;
б) если D<0, то в точке М0 экстремума нет;
в) если D=0, то требуются дополнительные исследования.
|
Производная по направлению
Вектор направления 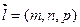 ;
Орт направления: ;
Орт направления:
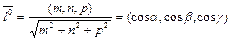 ;
Производная по направлению равна скалярному произведению градиента на орт направления: ;
Производная по направлению равна скалярному произведению градиента на орт направления:

| ||
Производные сложных функций
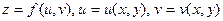 ;
u, v – промежуточные аргументы, x,.y – основные аргументы. ;
u, v – промежуточные аргументы, x,.y – основные аргументы.
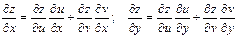
| Уравнение касательной плоскостик поверхности F (x,y,z) =0 в точке М0 (х0,у0,z0)
Скалярное произведение  ,
или ,
или

| Алгоритм нахождения наибольшего и наименьшего значений функции двух переменных в ограниченной замкнутой области 1. Найти точки, принадлежащие области, в которых частные производные первого порядка равны нулю или не существуют. Вычислить значения функции в этих точках. 2. Заменить одну из независимых переменных из уравнения границы области и найти наибольшее и наименьшее значения получившейся функции одного аргумента на отрезке изменения этого аргумента: вычислить значения функции в критических точках первого порядка и на концах отрезка. 3. Из всех полученных значений функции выбрать наибольшее и наименьшее. |
Производные неявно заданных функций
F (x,y,z) = 0, Û z = f (x,y).
 . .
| Уравнение нормалик
поверхности F (x,y,z) =0 в точке М0 (х0,у0,z0)
векторное произведение  ,
или ,
или

| |
Полный дифференциал ФНП
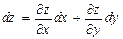 .
Полный дифференциал ФНП равен сумме ее частных дифференциалов: .
Полный дифференциал ФНП равен сумме ее частных дифференциалов:  . .
|
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 457; Нарушение авторских прав?; Мы поможем в написании вашей работы!