КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Длина вектора в ортонормированном базисе равна корню квадратному из суммы квадратов координат этого вектора. Например, если то . – проекция вектора на вектор
|
|
|
|
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Координаты вектора  находят, вычитая из координат точки
находят, вычитая из координат точки  , являющейся концом вектора, соответствующие координаты точки
, являющейся концом вектора, соответствующие координаты точки  , являющейся началом вектора.
, являющейся началом вектора.
 =
=  .
.
Косинус угла между векторами 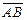 и
и  равен отношению скалярного произведения этих векторов к произведению длин этих векторов:
равен отношению скалярного произведения этих векторов к произведению длин этих векторов: 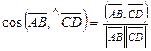 .
.
Скалярное произведение двух векторов в ортонормированном (декартовом) базисе равно сумме произведений одноименных координат этих векторов: если 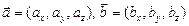 , то
, то  .
.
В ортонормированном базисе векторное произведение находят, раскладывая определитель, в первой строке которого – орты  декартовой системы координат, во второй строке – координаты левого из перемножаемых векторов, а в третьей строке – координаты правого из перемножаемых векторов.
декартовой системы координат, во второй строке – координаты левого из перемножаемых векторов, а в третьей строке – координаты правого из перемножаемых векторов.
 Например,
Например, 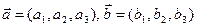 , тогда векторное произведение этих векторов в декартовой системе координат можно найти так: Свойства векторного произведения
, тогда векторное произведение этих векторов в декартовой системе координат можно найти так: Свойства векторного произведения
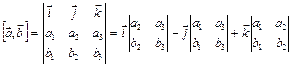 .
. 
| Геометрический смысл векторного произведения. | Модульвекторного произведениячисленно равенплощади параллелограмма,построенного на перемножаемых векторах как на двух смежных сторонах. Обычно векторы приводят к общему началу. Половина модулявекторного произведениячисленно равнаплощади треугольника,построенного на перемножаемых векторах как на двух смежных сторонах этого треугольника. Обычно векторы приводят к общему началу. |
| Определение и условие компланарности векторов. | Векторы, лежащие в одной или параллельных плоскостях, называются компланарными. Смешанноепроизведение ненулевых компланарныхвекторов равно нулю. |
Смешанное произведение трех векторов получают, умножая векторное произведение двух векторов на третий вектор скалярно.
В ортонормированном базисе смешанное произведение равно определителю, строками или столбцами которого являются координаты перемножаемых векторов. Обычно первой строкой определителя записывают координаты первого вектора, второй строкой – координаты второго вектора, а третьей строкой – координаты третьего вектора, если считать векторы слева направо.
Полезно помнить такие свойства смешанного произведения: 1) при перестановке двух любых соседних векторов смешанное произведение меняет знак на противоположный; 2) при циклической перестановке (последний вектор ставится впереди первого) смешанное произведение не изменяется, поскольку при этом два раза переставляются соседние векторы.
| Геометрический смысл смешанного произведения. Деление отрезка в отношении λ. | Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах как на ребрах. Обычно векторы приводят к общему началу. Объём пирамиды, построенной на векторах  , ,  и и  , равен одной шестой объёма параллелепипеда, построенного на этих же векторах как на ребрах , равен одной шестой объёма параллелепипеда, построенного на этих же векторах как на ребрах
 : :  . .
|
ГЕОМЕТРИЯ ПРЯМЫХ И ПЛОСКОСТЕЙ В ТАБЛИЦАХ
Уравнения плоскости Р в трехмерном пространстве R 3 и уравнения прямой L
в двухмерном пространстве R 2
Таблица 1
| Уравнения плоскости Р в R 3 в координатной форме | Векторная форма уравнений P, L в R 3 и R 2 | Уравнения прямой L в R 2 в координатной форме | ||||||||
| I R 3 Уравнения P и L, проходящих через данную точку М 1 R 2I перпендикулярно данному вектору N | ||||||||||
  N =(A, B, C)
r = (x,y,z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1 ,z 1)Î P
" M (x,y,z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0 N =(A, B, C)
r = (x,y,z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1 ,z 1)Î P
" M (x,y,z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0
| r-r 1 = M 1 M M 1 M ^ N (P) M 1 M ^ N (L) (r-r 1, N) = 0 (M 1 M, N) = 0 Условие ортогональности векторов | N = (A,B) r = (x,y) r 1 = (x 1, y 1) M (x 1, y 1) Î L " M (x,y) Î L A (x-x 1)+ B (y-y 1) = 0 | ||||||||
| II R 3 Общие уравнения R 2 II | ||||||||||
| Ax + By + Cz + D = 0 D = -Ax 1 - By 1 - Cz 1 | (r,N) + D = 0 D = – (r1, N) | Ax + By +D = 0 D = -Ax 1 -By 1 | ||||||||
| III R3 Через n фиксированных точек M R2 III | ||||||||||
| n = 3 | n = 2 | |||||||||
M 1(x 1 ,y 1, z, 1)Î P, М 1 М Î Р
M 2(x 2, y 2, z 2)Î P, М 2 М 1Î Р
M 3(x 3, y 3, z 3)Î P, М 3 М 1Î Р
" M (x,y,z)Î P  

| M 1 Î P, L M 2 Î P, L " M Î P, L M 3 Î P | M 1(x1,y1) Î L,
M 2(x2,y2) Î L
" M (x,y) Î L
М 1 М çç М 2 М 1
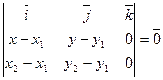

| ||||||||

| (M 1 M, M 1 M 2, M 1 M 3)=0 Условие компланарности векторов | [ M 1 M, M 1 M 2] = 0 Условие коллинеарности векторов | ||||||||


| A =y 2 -y 1; B = – (x 2 -x 1), Û A (x-x 1) + B (y-y 1) = 0 (1. I.) | |||||||||
| IV R 3 Уравнения в отрезках R 2 IV | ||||||||||
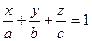 y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
| r = xi+yj+zk t = i/a +j/b +k/c (r,t) = 1 t = (1 /a, 1 /b, 1 /c) ç r ç cos (r,t) = 1/ ç t ç |

 y= 0 Þ x=a
x= 0 Þ y=b y= 0 Þ x=a
x= 0 Þ y=b
| ||||||||
Уравнения прямой L в трехмерном пространстве R 3 и в двухмерном пространстве R 2
Таблица 2
| Уравнения прямой L в R 3 в координатной форме | Векторная форма уравнений прямой L в R 2 и R 3 | Уравнения прямой L в R 2 в координатной форме | |||
| I Канонические уравнения прямой L I | |||||
  l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L
 
| r-r 1= M 1 M çç l r 2- r 1= M 1 M 2 çç l [ r-r 1, l ]=0 [ M 1 M, l ]=0 | l =(m,n)
l =(m,n) çç L
M 1(x 1, y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L

| |||
| II Параметрические уравнения прямой L II | |||||
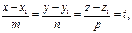 " t Î R 1 " t Î R 1
 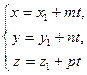

| r-r 1 çç l, " t Î R 1 M 1 M çç l r-r 1= M 1 M = tl r=r 1+ tl [ M 1 M, tl ]=0 |
 " t Î R 1 " t Î R 1
  
| |||
| III Уравнения прямой L, проходящей через две данные точки M 1 и M 2 III | |||||
l çç L, l=(m,n,p), lt = M 1 M 2
m=x 2– x 1, n=y 2– y 1, p=z 2– z 1
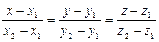
| M 1 M çç M 1 M 2 çç l M 1Î L, M 2Î L, " M Î L [ M 1 M, M 1 M 2]=0 |
l çç L, l =(m,n), tl = M 1 M 2
m=x 2– x 1, n = y 2-– y 1
.
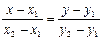

| |||
| IV Общие уравнения прямой L в R 3 (P 1Ç P 2) | Уравнение прямой L с угловым коэффициентом k в R 2 V | ||||
 N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0. N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0.
|
A x+ B y+ D =0, B ¹0
ß

 y = kx + b y = kx + b 
 a³0 a³0
| ||||
таблица 2 а (продолжение таблицы 2)
| Связь между уравнениями прямой L в R 3 | Связь между уравнениями прямой L в R 2 |
 Общие(2.IV) Общие(2.IV)

 Þ z0=0 Þ z0=0
 Þ M 0(x 0, y 0,0)Î L
или Þ M 0(x 0, y 0,0)Î L
или  Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или  Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p) Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p)
 – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß
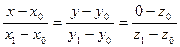 – через две
точки M 0Î L, M 1Î L (2.III) – через две
точки M 0Î L, M 1Î L (2.III)
 – общие(2.IV) – общие(2.IV)
| С угловым коэффициентом: (2.V)
y = kx+b  ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.
ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.

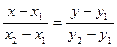 через точки M 1Î L и M 2Î L
(1. III) (2.III) через точки M 1Î L и M 2Î L
(1. III) (2.III)
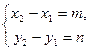 Þ Þ  – канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
– канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
|
Взаимное расположение плоскостей P в трёхмерном пространстве R 3
и прямых L в двухмерном пространстве R2
ТАБЛИЦА 3
| I Обозначения, принятые в таблице 2, {P1,P2} в R3 | I | Обозначения, принятые в I таблице 2, {L1,L2} в R2 | |||
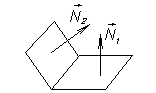  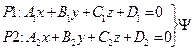 N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)


| R3 cos j = 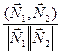 N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1 =(A 1, B 1) N 2 =(A 2, B 2)
| a)  N1=(A1,B1);N2=(A2,B2)
N1=(A1,B1);N2=(A2,B2)

 б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j =
б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j =  ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) =
ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) = 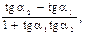
| |||
| II Признаки взаимного расположения плоскостей {P1, P2} и прямых {L1, L2} II | |||||
| плоскости { Р 1, Р 2} в R n; n =3 | Как расположены P и L | Прямые { L 1, L 2} в R n; n =2 | |||
P 1 Ç P 2 (пересекаются)
cos j= 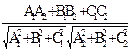 ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y) ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y)
|  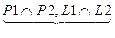 N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
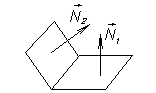 cos j ≠ ± 1 cos j ≠ ± 1
| L 1Ç L 2 (пересекаются)
a)  L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=
L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j= 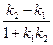 ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c) ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c)
| |||
P 1ïï P 2 (параллельны)
 cos j = ±1
cos j = ±1
| 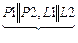 N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
| L 1ïï L 2 (параллельны)
а) 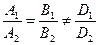 cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
| |||
P 1º P 2 (совпадают)
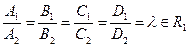 cosj = ±1
cosj = ±1
|  N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
| L 1º L 2 (совпадают)
а)  cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
|
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 2822; Нарушение авторских прав?; Мы поможем в написании вашей работы!



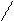 N 1 çç N 2 Û P 1Ç P 2 Û Rang
N 1 çç N 2 Û P 1Ç P 2 Û Rang