
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление определителей
|
|
|
|
Правило треугольников для вычисления определителей третьего порядка:
|

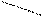
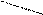
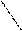








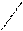
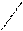
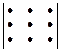
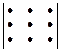
+ –
Таблица Саррюса для вычисления определителей третьего порядка:
1 2 3 1 2 ─ столбцы.



















 |  | ||||||
 | |||||||
 | |||||||
Правило разложения определителя по элементам какой-либо его строки или столбца с использованием понятия минора и алгебраического дополнения
Определение
минора 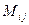 элемента
элемента  определителя
n -го порядка.
определителя
n -го порядка.
| Минором  элемента элемента 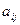 определителя n- го порядка называется
определитель (n– 1 )- го порядка, полученный из данного определителя вычеркиванием элементов i- й строки и j- го столбца. определителя n- го порядка называется
определитель (n– 1 )- го порядка, полученный из данного определителя вычеркиванием элементов i- й строки и j- го столбца.
|
Определение алгебраического дополнения 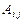 элемента элемента  определителя n -го порядка. определителя n -го порядка.
| Алгебраическим дополнением 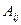 элемента элемента 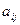 называется минор этого элемента, умноженный на называется минор этого элемента, умноженный на 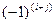 : :
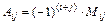
|
В соответствии со свойствами определитель порядка n может быть представлен в виде разложения этого определителя по элементам i- й строки:

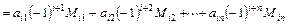 .
.
То есть определитель квадратной матрицы А порядка n равен сумме произведений элементов какой-либо i-й его строки на алгебраические дополнения этих элементов.
Аналогичным образом можно разложить этот же определитель по элементам любого его столбца.
Так для определителя третьего порядка формула разложения определителя по элементам второго столбца получится следующей:

 =
=
=  .
.
Определители второго порядка получаются, если вычеркнуть в определителе третьего порядка второй столбец и, соответственно, первую, потом вторую, потом третью строки.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 508; Нарушение авторских прав?; Мы поможем в написании вашей работы!