
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расширенный алгоритм Евклида
|
|
|
|
Асимметричная криптосистема RSA.
Пояснение к заданию 3
- Выбирают два больших простых числа p и q. Для большей криптостойкости p и q выбирают равной длины.
- Вычисляют произведение: n=pq
- Вычисляют z=(p-1)(q-1) и выбирают число е взаимно простое с z, т.е. НОД (е,z)=1.
- Для вычисления закрытого (секретного) ключа d решается сравнение
еd 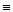 1modz (1)
1modz (1)
Решение (1) имеет вид 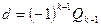
Для вычисления ключа d воспользуемся расширенным алгоритмом Евклида. Для этого число 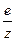 обращается в конечную цепную дробь:
обращается в конечную цепную дробь:
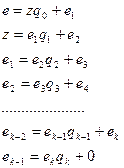
Цепная дробь имеет вид: 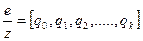 , а последовательности
, а последовательности 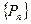 и
и 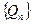 числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
числителей и знаменателей подходящих дробей к цепной дроби определяются рекуррентно:
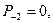
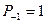 ,
, 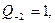
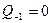 .
.
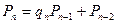 ,
, 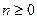
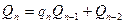 ,
, 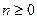
Их вычисления удобно оформить в виде таблицы:
| n | -2 | -1 | ……………. | k-1 | k | |||
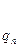
| 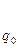
| 
| 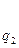
| 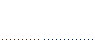
| 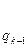
| 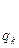
| ||
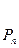
| 
| 
| 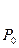
| 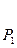
| 
| 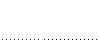
| 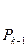
| 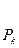
|
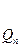
| 
| 
| 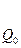
| 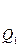
| 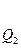
| 
| 
| 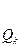
|
Задача 3.1.
Пусть выбраны простые числа р =47 и q=71 и открытый ключ е=79.
Требуется выполнить шифрование и дешифрование в асимметричной криптосистеме RSA сообщения:
688 232 687 966 668 3
Укажите последовательность операций.
Решение.
1. 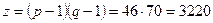
2. Найдём секретный ключ 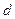 в результате решения сравнения:
в результате решения сравнения:
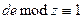 ,
,
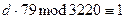 .
.
Воспользуемся расширенным алгоритмом Евклида:
79=3220*0+79,
3220=79*40+60,
79=60*1+19,
60=19*3+3,
19=3*6+1,
3=1*3+0.
Результаты вычислений сведём в таблицу:

| 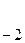
| 
| 
| 
| 
| 
| 
| 
|
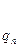
| 
| 
| 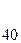
| 
| 
| 
| 
| |
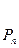
| 
| 
| ||||||
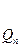
| 
| 
| 
| 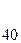
| 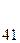
| 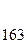
| 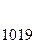
| 
|
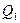
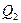
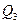
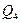
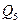 .
.
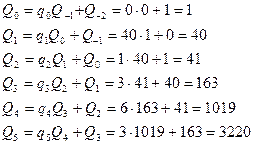
к=5 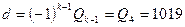
В самом деле 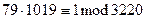
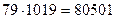 ,
,
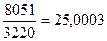

Следовательно, d =1019.
- Разобьём сообщение на блоки mi, которые должны иметь длину, меньшую, чем п= pq = 47.17 =3337.

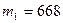 ,
, 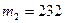 ,
, 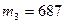 ,
, 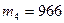 ,
, 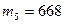 ,
, 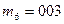
- Затем шифруем блоки:
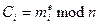
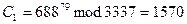 , и т.д.
, и т.д.
Получим криптограмму: С=(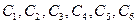 ) =
) =
=1570  2756 2091 2276 2423 0158
2756 2091 2276 2423 0158
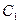
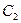
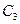
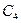
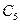
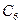 .
.
5. Для дешифрования нужно выполнить возведение в степень, используя ключ дешифрования d, т.е. 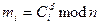
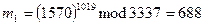 и т.д.
и т.д.
Задача 3.2.
Зашифровать и расшифровать сообщение САВ. Для простоты вычислений использовать небольшие числа: р =3, q=11, открытый ключ е=7. Для вычисления секретного ключа d воспользоваться расширенным алгоритмом Евклида.
Решение.
Действия пользователя В- получателя сообщения.
1. Выбирает р =3 и q=11.
2. Вычисляет модуль n=p*q=3*11=33.
3. Вычисляет значение функции Эйлера для n = 33:
z (33) = (p –1)(q –1) = 2*10 = 20.
Выбирает в качестве открытого ключа е произвольное число с учетом выполнения условий:
1< 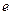 £ 20, НОД (e, 20) = 1.
£ 20, НОД (e, 20) = 1.
Пусть e = 7.
4. Вычисляет значение секретного ключа d, используя расширенный алгоритм Евклида при решении сравнения
d 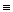 7–1 (mod 20).
7–1 (mod 20).
Решение дает d = 3.
5. Пересылает пользователю А (отправителю) пару чисел (n = 33, e = 7).
Действия пользователя A-отправителя сообщения.
6. Представляет шифруемое сообщение как последовательность целых чисел в диапазоне 0... 32. Пусть буква А представляется как число 1, буква В – как число 2, буква С – как число 3. Тогда сообщение САВ можно представить как последовательность чисел 312, т.е. 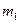 = 3,
= 3, 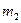 = 1,
= 1, 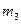 = 2.
= 2.
7. Шифрует текст, представленный в виде последовательности чисел 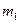 ,
, 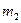 и
и 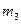 , используя ключ e = 7 и n = 33, по формуле
, используя ключ e = 7 и n = 33, по формуле
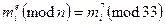
Получает криптограмму:
С1 = 37 (mod 33) = 2187 (mod 33) = 9,
С2 =1 7 (mod 33) =1 (mod 33) =1,
С3 = 27 (mod 33) =128 (mod 33) = 29.
Отправляет пользователю В криптограмму
С1, С2, С3 = 9, 1, 29.
Действия пользователя В.
8. Расшифровывает принятую криптограмму С1, С2, С3, используя секретный ключ d =3, по формуле
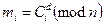
Получает:
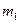 = 93 (mod 33) = 729 (mod 33) = 3,
= 93 (mod 33) = 729 (mod 33) = 3,
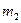 =13 (mod 33) =1 (mod 33) =1,
=13 (mod 33) =1 (mod 33) =1,
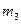 = 293 (mod 33) = 24389 (mod 33) = 2.
= 293 (mod 33) = 24389 (mod 33) = 2.
Таким образом, восстановлено исходное сообщение: С А В
3 1 2
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 2925; Нарушение авторских прав?; Мы поможем в написании вашей работы!