Хеллмана

Распределение ключей в компьютерной сети

Пояснение к заданию 5

При использовании для информационного обмена криптосистемы с симметричным секретным ключом два пользователя, желающие обменяться криптографически защищенной информацией, должны обладать общим секретным ключом. Пользователи должны обменяться общим ключом по каналу связи безопасным образом. Если пользователи меняют ключ достаточно часто, то доставка ключа превращается в серьезную проблему.

Для решения этой проблем можно применить два способа:

1) использование криптосистемы с открытым ключом для шифрования и передачи секретного ключа симметричной криптосистемы;

2) использование системы открытого распределения ключей Диффи–Хеллмана.

5.1. Алгоритм открытого распределения ключей Диффи–

Алгоритм Диффи–Хеллмана был первым алгоритмом с открытыми ключами (предложен в 1976 г.). Его безопасность обусловлена трудностью вычисления дискретных логарифмов в конечном поле, в отличие от легкости дискретного возведения в степень в том же конечном поле.

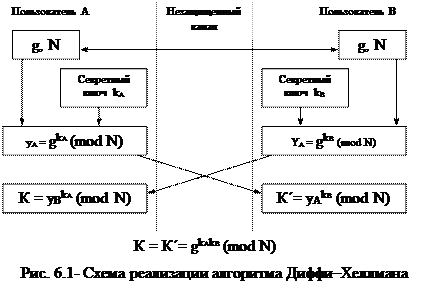
Предположим, что два пользователя А и В хотят организовать защищенный коммуникационный канал.

1. Обе стороны заранее уславливаются о модуле N (N должен быть простым числом) и примитивном элементе g, (1 £ g £ N –1).

Эти два целых числа N и g могут не храниться в секрете. Как правило, эти значения являются общими для всех пользователей системы.

2. Затем пользователи А и В независимо друг от друга выбирают собственные секретные ключи k_А и k_В (k_А и k_В – случайные большие целые числа, которые хранятся пользователями А и В в секрете).

3. Далее пользователь А вычисляет открытый ключ

y_A = (mod N),

а пользователь В – открытый ключ

y_В = 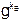(mod N).

4. Затем стороны А и В обмениваются вычисленными значениями открытых ключей y_A и y_В по незащищенному каналу.

5. Далее пользователи А и В вычисляют общий секретный ключ, используя следующие выражения:

пользователь А: К = 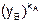= 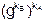(mod N);

пользователь В: К´ = = 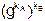(mod N).

При этом К = К´, так как 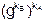= 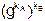(mod N).

Схема реализации алгоритма Диффи–Хеллмана показана на рис. 6.1.

Ключ К может использоваться в качестве общего секретного ключа (ключа шифрования ключей) в симметричной криптосистеме. Кроме того, обе стороны А и В могут шифровать сообщения, используя следующее преобразование шифрования (типа RSA): С = Е_K (М) = М^К (mod N).

Для выполнения расшифрования получатель сначала нахо-

дит ключ расшифрования К* с помощью сравнения

К * К* º 1 (mod N –1),

а затем восстанавливает сообщение

М = D_K (C) = C^K*(mod N).

Задача 5.1

Реализовать алгоритм открытого распределения ключей Диффи-Хеллмана при следующих начальных условиях: модуль N=47, примитивный элемент g=23, секретные ключи пользователей А и В: K_А=12, К_В=33 соответственно.

Решение. Для того, чтобы иметь общий секретный ключ К, пользователи А и В сначала вычисляют значения частных открытых ключей:

y_A = 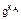(mod N)= 23¹²(mod 47) = 27,

y_В = 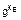(mod N)= 23³³(mod 47) = 33

После того, как пользователи А и В обменяются своими значениями y_A и y_В , они вычисляют общий секретный ключ

К = 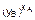(mod N)= 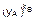(mod N)= 33¹²(mod 47)= 27³³ (mod 47)= =23^12*33 (mod 47)= 25.

Кроме того, они находят секретный ключ расшифрования, решая следующее сравнение:

К * К* º 1 (mod N –1),

откуда К* = 35.

Если сообщение М =16, то криптограмма:

С = М^К =16²⁵(mod 47) = 21.

Получатель восстанавливает сообщение:

М = С^К* = 21³⁵(mod 47) =16.

Злоумышленник, перехватив значения N, g, y_А и y_В, тоже хотел бы определить значение ключа К. Очевидный путь для решения этой задачи состоит в вычислении такого значения k_А по N, g, y_А, что mod N = y_А (поскольку в этом случае, вычислив k_А, можно найти К= 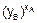mod N). Однако нахождение k_А по N, g и y_А – задача нахождения дискретного логарифма в конечном поле, которая считается неразрешимой.

Выбор значений N и g может иметь существенное влияние на безопасность этой системы. Модуль N должен быть большим и простым числом. Число (N –1)/2 также должно быть простым числом. Число g желательно выбирать таким, чтобы оно было примитивным элементом множества Z_N.

Алгоритм открытого распределения ключей ДиффиХеллмана позволяет обойтись без защищенного канала для передачи ключей. Однако, работая с этим алгоритмом, необходимо иметь гарантию того, что пользователь А получил открытый ключ именно от пользователя В, и наоборот. Эта проблема решается с помощью электронной подписи, которой подписываются сообщения об открытом ключе.

Дата добавления: 2015-06-27