Квадратичные вычеты

Основные способы нахождения обратных величин

a^–1 º 1 (mod n).

1. Проверить поочередно значения 1, 2,..., n – 1, пока не будет найден a^–1 º1 (mod n), такой, что a*a^–1 (mod n) º 1.

2. Если известна функция Эйлера j(n), то можно вы-числить

a^–1 (mod n) º a^j(n)–1 (mod n),

используя алгоритм быстрого возведения в степень.

3. Если функция Эйлера j(n) не известна, можно использовать расширенный алгоритм Евклида.

Проиллюстрируем эти способы на числовых примерах.

1. Поочередная проверка значений 1, 2,..., n – 1, пока не будет найден x = a^–1 (mod n), такой что a * x º 1 (mod n).

Пусть n = 7, a = 5. Требуется найти x = a^–1 (mod n).

a * x º 1 (mod n) или 5 * x º 1 (mod 7).

n – 1 = 7 – 1 = 6.

Получаем x = 5^–1 (mod 7) = 3.

Результаты проверки сведены в табл. П.2.

Таблица П.2

x	5 * x	5 * x (mod 7)
3		1

2. Нахождение a^–1 (mod n), если известна функция Эйлера j(n).

Пусть n = 7, a = 5. Найти x = a^–1 (mod n) = 5^–1 (mod 7). Модуль n = 7 – простое число. Поэтому функция Эйлера j(n) = j(7) = = n –1 = 6. Обратная величина от 5 по mod 7

a^–1 (mod n) = a^j(n)–1 (mod n) =

= 5^6–1 mod 7 = 5⁵ mod 7 = (5² mod 7)(5³ mod 7) mod 7 =

= (25 mod 7)(125 mod 7) mod 7 = (4 * 6) mod 7 = 24 mod 7 = 3.

Итак, x = 5^–1 (mod 7) = 3.

3. Нахождение обратной величины a^–1 (mod n) с помощью расширенного алгоритма Евклида.

Алгоритм Евклида можно обобщить способом, который имеет большое практическое значение. При этом способе во время вычисления НОД (a,b) можно попутно вычислить такие целые числа u₁ и u₂, что

a * u₁ + b * u₂ = НОД (a,b).

Это обобщение (расширение) алгоритма Евклида удобно описать, используя векторные обозначения.

Рассмотрим некоторое простое p > 2 и число a < p. Если число a сравнимо с квадратом некоторого числа x по модулю p, т.е. выполняется сравнение x² º a (mod p), тогда a называют квадратичным вычетом по модулю p. В противном случае a называют квадратичным невычетом по модулю p.

Если a – квадратичный вычет, сравнение x² º a (mod p) имеет два решения: +x и –x, т.е. a имеет два квадратных корня по модулю p.

Все квадратичные вычеты находят возведением в квадрат элементов 1, 2, 3,..., (p –1)/2.

Не все значения a < p являются квадратичными вычетами. Например, при p = 7 квадратичные вычеты это 1, 2, 4:

1² = 1 º (mod 7),

2² = 4 º 4 (mod 7),

3² = 9 º 2 (mod 7),

4² =16 º 2 (mod 7),

5² = 25 º 4 (mod 7),

6² = 36 º1 (mod 7).

Заметим, что каждый квадратичный вычет появляется в этом списке дважды. Не существует никаких значений x, которые удовлетворяли бы любому из следующих уравнений:

x² º 3 (mod 7),

x² º 5 (mod 7),

x² º 6 (mod 7).

Числа 3, 5 и 6 – квадратичные невычеты по модулю 7. Можно доказать, что существует точно (p –1)/2 квадратичных вычетов по модулю p и (p –1)/2 квадратичных невычетов по модулю p.

Если a – квадратичный вычет по модулю p, то a имеет точно два квадратных корня: один корень между 0 и (p –1)/2, другой корень между (p –1)/2 и (p –1).

Один из этих квадратных корней также является квадратичным вычетом по модулю p; он называется главным квадратным корнем.

Вычиcление квадратных корней при p=7 представлено в табл. П.4.

Таблица П.4

x^2 º a (mod 7)	Корни
x1	x2
1^2 º 1(mod 7) 2^2 º 4(mod 7) 3^2 º 2(mod 7)	+1 +2 +3	–1 = –1 + 7 = 6 –2 = –2 + 7 = 5 –3 = –3 + 7 = 4

Если n – произведение двух простых p и q, т.е. n = p * q, то существуют точно

(p –1)(q –1)/4

квадратичных вычетов по модулю n, взаимно простых с n. Например, по модулю 35 (p = 5, q = 7, n = 5 * 7 = 35) существуют

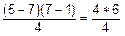= 6

квадратичных вычетов: 1, 4, 9, 11, 16, 29, взаимно простых с 35.

Дата добавления: 2015-06-27