
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модулярная арифметика
|
|
|
|
ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ
П Р И Л О Ж Е Н И Е
Модулярная арифметика часто изучается в школе как "арифметикачасов". Если отсчитать 14 часов от 3 часов после полудня, то получится 5 часов утра следующего дня:
3 +14 º 5 (mod 12)
или
(3 +14) mod 12 = 5.
Это арифметика по модулю 12.
Обычная запись в модулярной арифметике
a º b (mod n)
читается так: "a сравнимо с b по модулю n". Это соотношение справедливо дляцелых значений a,b и n ¹ 0, если, и только если
a = b + k * n
для некоторого целого k.
Отсюда, в частности, следует
n | (a – b).
Это читается как "n делит (a – b)".
Если a º b (mod n),
то b называют вычетом числа a по модулю n.
Операцию нахождения вычета числа a по модулю n
a (mod n)
называют приведением числа a по модулю n или приведением по модулю.
В нашем примере
(3 +14) mod 12 =17 mod 12 = 5
или
17 º 5 (mod 12),
число 5 является вычетом числа 17 по модулю 12.
Набор целых чисел от 0 до (n –1) называют полным набором вычетов по модулю n. Это означает, что для любого целого a (a > 0) его вычет r по модулю n есть некоторое целое число в интервале от 0 до (n –1), определяемое из соотношения
r = a – k * n,
где k – целое число.
Например, для n =12 полный набор вычетов:
{0, 1, 2, …, 11}.
Обычно предпочитают использовать вычеты
r Î {0, 1, 2, …, n –1},
но иногда полезны вычеты в диапазоне целых:
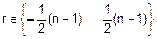 .
.
Заметим, что
–12 (mod 7) º –5 (mod 7) º 2 (mod 7) º 9 (mod 7) и т.д.
Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Точнее говоря, целые числа по модулю n с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.
Фактически мы можем либо сначала приводить по модулю n, а затем выполнять операции, либо сначала выполнять операции, а затем приводить по модулю n, поскольку приведение по модулю n является гомоморфным отображением из кольца целых в кольцо целых по модулю n:
(a + b) mod n = [a (mod n) + b (mod n)] mod n,
(a – b) mod n = [a (mod n) – b (mod n)] mod n,
(a * b) mod n = [a (mod n) * b (mod n)] mod n,
[a * (b + c)] mod n = {[a * b (mod n)] + [a * c (mod n)]} mod n.
Криптография использует множество вычислений по модулю n, потому что задачи типа вычисления дискретных логарифмов и квадратных корней очень трудны. Кроме того, с вычислениями по модулю удобнее работать, потому что они ограничивают диапазон всех промежуточных величин и результата.
Для модуля n длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее
2k бит. Поэтому возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов.
Вычисление степени числа a по модулю n
ax mod n
можно выполнить как ряд умножений и делений. Существуют способы сделать это быстрее. Поскольку эти операции дистрибутивны, быстрее произвести возведение в степень как ряд последовательных умножений, выполняя каждый раз приведение по модулю. Это особенно заметно, если работать с длинными числами (200 бит и более).
Например, если нужно вычислить
a8 mod n,
не следует применять примитивный подход с выполнением семи перемножений и одного приведения по модулю громадного числа:
(a * a * a * a * a * a * a * a) mod n.
Вместо этого выполняют три малых умножения и три малых приведения по модулю:
((a2 mod n)2 mod n)2 mod n.
Тем же способом вычисляют
a16 mod n = (((a2 mod n)2 mod n)2 mod n)2 mod n.
Вычисление
ax mod n,
где x не является степенью 2, лишь немного сложнее. Двоичная запись числа x позволяет представить число x как сумму степеней 2:
x = 25(10) ® 1 1 0 0 1(2), поэтому 25 = 24 + 23 + 20.
Тогда
a25 mod n = (a*a24) mod n = (a*a8 *a16) mod n =
= a * ((a2)2)2 * (((a2)2)2)2 mod n = ((((a2 * a)2)2)2 * a) mod n.
При разумном накоплении промежуточных результатов потребуется только шесть умножений:
(((((((a2 mod n) * a) mod n)2 mod n)2 mod n)2 mod n) * a) mod n.
Этот метод уменьшает трудоемкость вычислений до 1,5хk операций в среднем, где k – длина числа в битах.
Поскольку многие алгоритмы шифрования основаны на возведении в степень по модулю n, целесообразно использовать алгоритмы быстрого возведения в степень.
Вычисление обратных величин
В арифметике действительных чисел нетрудно вычислить мультипликативную обратную величину a–1 для ненулевого a:
a–1 =1/a или a * a–1 =1.
Например, мультипликативная обратная величина от числа 4 равна 1/4, поскольку
4 * 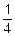 =1.
=1.
В модулярной арифметике вычисление обратной величины является более сложной задачей. Например, решение сравнения
4 * x º1 (mod 7)
эквивалентно нахождению таких значений x и k, что
4 * x º 7 * k +1,
где x и k – целые числа.
Общая формулировка этой задачи – нахождение такого целого числа x, что
a * x (mod n) =1.
Можно также записать
a–1 º x (mod n).
Решение этой задачи иногда существует, а иногда его нет. Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку
5 * 3 =15 º 1 (mod 14).
С другой стороны, число 2 не имеет обратной величины по модулю 14.
Вообще сравнение
a–1 º x (mod n)
имеет единственное решение, если a и n – взаимно простые числа.
Если числа a и n не являются взаимно простыми, тогда сравнение
a–1 º x (mod n)
не имеет решения.
Сформулируем основные способы нахождения обратных величин. Пусть целое число a Î {0, 1, 2, …, n – 1}.
Если НОД (a, n) =1, то a * i (mod n) при i= 0, 1, 2, …, n –1 является перестановкой множества {0, 1, 2, …, n – 1}.
Например, если a = 3 и n = 7 (НОД (3,7) =1), то
3 * i (mod 7) при i= 0, 1, 2, …, 6
является последовательностью 0, 3, 6, 2, 5, 1, 4, т.е. перестановкой множества {0, 1, 2, …, 6}.
Это становится неверным, когда НОД (a, n) ¹ 1. Например, если a = 2 и n = 6, то
2 * i (mod 6) º 0, 2, 4, 0, 2, 4 при i= 0, 1, 2, …, 5.
Если НОД (a,n) =1, тогда существует обратное число a–1, 0 < a–1 < n, такое, что
a * a–1 º1 (mod n).
Действительно, a * i (mod n) является перестановкой 0, 1,..., n –1, поэтому существует i,такое, что
a * i º1 (mod n).
Как уже отмечалось, набор целых чисел от 0 до n –1 называют полным набором вычетов по модулю n. Это означает, что для любого целого числа a (a > 0) его вычет r = a (mod n) – это некоторое целое число в интервале от 0 до n –1.
Выделим из полного набора вычетов подмножество вычетов, взаимно простых с n. Такое подмножество называют приведенным набором вычетов.
Пример. Пусть модуль n =11 – простое число. Полный набор вычетов по модулю 11
{0, 1, 2, …, 10}.
При формировании приведенного набора вычетов из них удаляется только один элемент – 0. Приведенный набор вычетов по модулю 11 имеет 11 – 1 = 10 элементов.
Вообще приведенный набор вычетов по модулю простого числа n имеет n –1 элементов.
Пример. Пусть модуль n =10. Полный набор вычетов по модулю n =10
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Из них только 1, 3, 7, 9 не имеют общего сомножителя с числом 10. Поэтому приведенный набор вычетов по модулю 10 равен {1, 3, 7, 9}. При формировании этого приведенного набора были исключены элементы:
0 (1 элемент),
кратные 2 (4 элемента),
кратные 5 (1 элемент),
т.е. всего шесть элементов. Вычитая их из 10, получаем 10 – 1 – 4 – 1 = 4, т.е. четыре элемента в приведенном наборе.
Для произведения простых чисел p * q = n приведенный набор вычетов имеет (p –1)(q –1) элементов. При n=p * q=2 * 5=10 число элементов в приведенном наборе
(p – 1)(q – 1) = (2 – 1) (5 –1) = 4.
Пример. Приведенный набор вычетов по модулю 27=33 имеет 18 элементов:
{1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26}.
Из полного набора вычетов исключены элементы, кратные 3 (всего девять элементов).
Для модуля в виде простой степени nr приведенный набор вычетов имеет nr–1 (n –1) элементов.
При n = 3, r = 3 получаем 33–1 (3 –1) = 32 * 2 =18.
Функция Эйлера j(n) характеризует число элементов в приведенном наборе вычетов (табл. П.1).
Таблица П.1
| Модуль n | Функция j(n) |
| n – простое n2 … nr | n –1 n (n –1) … nr–1 (n – 1) |
p * q (p, q – простые)
…
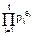 (pi – простые) (pi – простые)
| (p – 1) (q – 1)
…
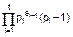
|
Иначе говоря, функция j(n) – это количество положительных целых, меньших n, которые взаимно просты с n.
Малая теорема Ферма: если n– простое и НОД (a,n)=1, то
an–1 º1 (mod n).
Согласно обобщению Эйлером малой теоремы Ферма имеем: если НОД (a,n) =1, то
aj(n) º1 (mod n).
Если n – простое число, то предыдущий результат, учитывая, что j(n) = n –1, приводится к виду (малой теоремы Ферма)
an–1 º1 (mod n).
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 7056; Нарушение авторских прав?; Мы поможем в написании вашей работы!