Ректор КГУ

Варианты задач для самостоятельного решения

Задача о распределении средств между предприятиями

Варианты задач для самостоятельного решения

Определить тип транспортной задачи. Если необходимо, привести к закрытому типу. Первоначальное распределение поставок выполнить методом наименьших затрат. Найти все оптимальные решения.

Задача 36.

Поставщики и их мощности	Потребители и их спрос
I (70)	II (65)	III (85)
I (55)
II (125)

Задача 37.

Поставщики и их мощности	Потребители и их спрос
I (120)	II (120)	III (100)
I (60)
II (90)
III (100)

Задача 38.

Поставщики и их мощности	Потребители и их спрос
I (45)	II (55)	III (60)
I (70)
II (30)
III (80)

Задача 39.

Поставщики и их мощности	Потребители и их спрос
I (90)	II (70)	III (100)
I (70)
II (80)
III (50)
IV (50)

Задача 40.

Поставщики и их мощности	Потребители и их спрос
I (50)	II (70)	III (60)	IV (20)
I (25)
II (40)
III (45)
IV (90)

4. Задачи динамического программирования

Динамическое программирование (ДП) – это метод оптимизации, разработанный для многошаговых операций, т.е. для таких операций, в которых процесс принятия решения может быть разбит на логические этапы. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить их решения в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений.

Общая постановка задачи, области применения моделей динамического программирования, принцип оптимальности и уравнения Беллмана рассмотрены в учебном пособии «Методы оптимальных решений». Рекомендуется повторить теоретический материал и пример решения задачи ДП из курса лекций перед тем, как приступить к решению задач.

Рассмотрим схему решения задач динамического программирования с использованием уравнений Беллмана на примере задачи о распределении средств.

Пример 15. Планируется деятельность трех предприятий на очередной год. Начальные средства, которые следует распределить, s₀=5 усл.ед. Размеры вложения в каждое предприятие кратны 1 усл.ед. Средства x, выделенные предприятию k, приносят в конце года прибыль f_k(x), k=1,2,3. Функции f_k(x) заданы таблично (табл. 36). Принято считать, что:

- прибыль f_k(x) не зависит от вложения средств в другие предприятия;

- прибыль выражается в одних условных единицах;

- общая прибыль равна сумме прибылей, полученных от каждого предприятия.

Определить, какое количество средств нужно выделить каждому предприятию, чтобы общая прибыль была наибольшей.

Таблица 36. Эффективность использования средств

x	f1(x)	f2(x)	f3(x)

Решение. Построим математическую модель задачи. Обозначим через x_k количество средств, выделенных предприятию k. Общая прибыль равна

(4.1)

Переменные x_k удовлетворяют ограничениям:

(4.2)

Требуется найти переменные x₁, x₂, x₃, удовлетворяющие системе ограничений (4.2), при которых функция (4.1) достигает максимума.

Особенность модели состоит в том, что хотя ограничения линейные и переменные целочисленные, методы целочисленного линейного программирования применять нельзя, так как функции f_k(x) заданы таблично.

Схема решения задачи методом динамического программирования имеет следующий вид:

- процесс распределения средств s₀=5 можно рассматривать как трехшаговый, номер шага совпадает с номером предприятия;

- выбор переменных x₁, x₂, x₃ – управление соответственно на I, II и III шаге;

- – конечное состояние процесса распределения, все средства вложены в производство.

Графически схема распределения показана на рис.1.

Уравнения состояний имеют вид:

(4.3)

где s_k – параметр состояния, количество средств, оставшихся после k -го шага, т.е. эти средства остается распределить между (3 – k) оставшимися предприятиями.

Рассмотрим функцию – условную оптимальную прибыль, полученную от предприятий k, (k+1),…,3, если между ними оптимальным образом распределялись средства . Допустимые управления на шаге k удовлетворяют условию: .

Уравнения, связывающие оптимальную прибыль на каждом шаге, имеют вид:

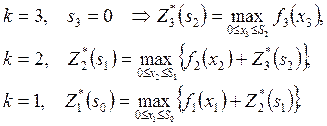(4.4)

Последовательно решает уравнения, проводя условную оптимизацию каждого шага (см. рис.1).

III шаг. В табл. 36 прибыль f₃(x) монотонно возрастает, поэтому все средства, оставшиеся к III шагу, следует вложить в предприятие 3. При этом для возможных значений s₂=0,1,…5 получим:

(4.5)

II шаг. Делаем все предположения относительно остатка средств s₁ ко II шагу, т.е. после выбора x₁. s₁ может принимать значения 0, 1, 2, 3, 4, 5. В зависимости от этого выбираем , находим и сравниваем для разных 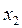при фиксированном 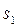значения суммы . Для каждого 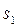наибольшее из этих значений - условная оптимальная прибыль, получаемая при оптимальном распределении средств между 2-м и 3-м предприятиями. Оптимизация записана в табл.37 при k=2. Для каждого значения 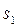оптимальные значения и записаны в графах 5 и 6.

I шаг. Условная оптимизация проведена в табл.37 при k=1 для значения s₀=5. Например, если x₁=0, то s₁=5, прибыль, полученная от трех предприятий при условии, что s₁=5 ед. средств между оставшимися двумя предприятиями будут распределены оптимально, равна 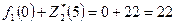. Значение взято из столбца 6 табл.37 при s₁=5. Если x₁=1, то s₁=4, суммарная прибыль при условии оптимального распределения ресурсов равна . Значение взято из табл.36, - из столбца 6 табл.37 при s₁=4. Аналогично вычислены остальные значения столбца 8 табл.37.

Оптимальное решение выделено в табл.37 жирным курсивом: максимум суммарной прибыли 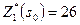при условии, что предприятию 1 выделена 1 усл.ед., предприятию 2 – 1 усл.ед., предприятию 3 – 3 усл.ед.

Достоинством метода является возможность анализа решения на чувствительность к изменению s₀ и числа шагов (предприятий), а также безразличие метода к способу задания функций .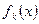

Таблица 37. Оптимизация распределения ресурсов

sk-1	xk	sk	k=2	k=1
			0+4=4			0+6=6
		6+0=6			8+0=8
			0+8=8			0+10=10
		6+4=10			8+6=14
		9+0=9			10+0=10
			0+12=12			0+14=14
		6+8=14			8+10=18
		9+4=13			10+6=16
		12+0=12			12+0=12
			0+16=16			0+18=18
		6+12=18			8+14=22
		9+8=17			10+10=20
		12+4=16			12+6=18
		15+0=15			14+0=14
			0+20=20			0+22=22
		6+16=22			8+18=26
		9+12=21			10+14=24
		12+8=20			12+10=22
		15+4=19			14+6=20
		18+0=18			16+0=16

Найти оптимальные решения задач.

Задача 41.

Решить задачу об оптимальном распределении ресурсов в количестве 6 усл.ед. между 3 предприятиями. Эффективность использования средств задана в табл.38.

Таблица 38. Эффективность использования средств

x	f1(x)	f2(x)	f3(x)

Задача 42.

Определить такой путь из пункта А в пункт Б, общая стоимость передвижения по которому будет минимальной.

Заключение

Рассмотренные методы решения могут быть применены для решения большого круга различных по физической и экономической природе задач.

Правильное построение экономико-математической модели задачи, понимание физического и экономического смысла искомых решений является необходимым условием для получения правильного, адекватного решения.

Литература

1. Исследование операций в экономике: Учеб.пособие для вузов / Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред.проф. Н.Ш.Кремера. – М.: ЮНИТИ, 2005.

2. Экономико-математические методы и модели. Задачник: уч.-метод. пособие / кол.авторов; под ред. С.И.Макарова, С.А.Севастьяновой. – М.: КНОРУС, 2008. – 208 с.

3. Вентцель, Е.С. Исследование операций. /Е.С.Вентцель. – М.: Сов. радио, 1972.

4. Просветов, Г.И. Методы оптимизации. Учебно-практическое пособие / Г.И.Просветов. - М.: Изд-во «Альфа-Пресс», 2009. - 168 с.

5. Лукиных, И.Г. Методы оптимальных решений. Учебное пособие /И.Г.Лукиных. – Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. – 63 с.

Содержание

Введение. 3

1. Задачи линейного программирования. 3

1.1. Решение задачи на максимум линейной функции. 4

1.2. Варианты задач для самостоятельного решения. 7

1.3. Отыскание минимума линейной функции. 9

1.4. Варианты задач для самостоятельного решения. 12

1.5. Особые случаи симплексного метода. 15

1.6. Варианты задач для самостоятельного решения. 20

1.7. Метод искусственного базиса (М-метод) 24

1.8. Варианты задач для самостоятельного решения. 27

2. Двойственные задачи. 30

Симметричная пара. 30

Несимметричная пара. 31

Смешанная пара. 32

2.1. Варианты задач для самостоятельного решения. 32

2.2. Экономическая интерпретация двойственной задачи. 33

2.3. Решение двойственной задачи и определение интервалов устойчивости двойственных оценок оптимального решения. 36

2.4. Варианты задач для самостоятельного решения. 38

2.5. Задачи целочисленного программирования. 39

2.6. Варианты задач для самостоятельного решения. 42

3. Транспортная задача. 44

3.1. Постановка и решение транспортной задачи. 44

3.2. Проверка плана на оптимальность. Метод потенциалов. 48

3.3. Варианты задач для самостоятельного решения. 54

4. Задачи динамического программирования. 56

4.1. Задача о распределении средств между предприятиями. 56

4.2. Варианты задач для самостоятельного решения. 61

Заключение. 62

Литература. 62

Содержание. 63

Учебное издание

Лукиных Ирина Григорьевна

МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ

Учебно-методическое пособие

Подписано в печать. Печать цифровая. Бумага для офисной техники.

Усл. печ. л.. Тираж 50 экз. Заказ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Вятский государственный университет»

610000, Киров, ул. Московская, 36, тел.: [phone], http://vyatsu.ru

___ __ Рассадин Н.М.

«_» _____________ 2010 г.

ПРОГРАММА ДИСЦИПЛИНЫ

Методы оптимальных решений

(в рамках национально-регионального (вузовского) компонента блок ЕН.Р)

Направление подготовки 080100.62 – Экономика

Профиль подготовки _________________

Дата добавления: 2015-06-27