Принципы выбора оптимальных стратегий в статистической игре

ОПТИМАЛЬНЫЕ РЕШАЮЩИЕ ПРАВИЛА

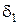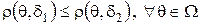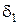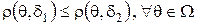Естественное упорядочение решающих правил по величине риска: решающее правило не хуже правила , если ; решающее правило лучше правила , если , и 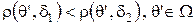; решающее правило 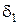эквивалентно правилу , если .

Класс решающих правил 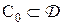называют полным, если для любого правила, не принадлежащего этому классу, существует лучшее правило в .

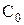Класс решающих правил 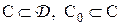называют существенно полным, если для любого , существует , которое не хуже, чем .

Основным теоретико-игровым принципом выбора оптимального решающего правила 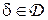на основе упорядочения стратегий статистика по величине риска 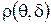при неизвестной стратегии природы 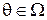, является выбор правила, минимизирующего максимальный риск.

Решающее правило называется минимаксным, если

.

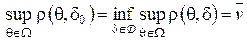Оптимальная максиминная стратегия природы, называемая наименее благоприятным априорным распределением, 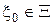, имеет место, если

.

Полезным приёмом при отыскании оптимальных стратегий статистика в статистической игре с природой является упорядочение решающих правил по величине байесовского риска 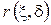относительно некоторого априорного распределения .

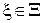Решающее правило 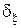называется байесовским относительно 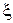, если

.

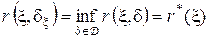Выражение в правой части называют минимальным байесовским риском.

Заметим, что если соответствующие внешние экстремумы не достигаются, то могут рассматриваться подходящие минимизирующие (максимизирующие) последовательности или 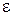-оптимальные стратегии.

Если распределения 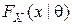дискретны или абсолютно непрерывны при любых 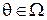, а пространства 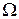и A компактны в смысле естественной метрики, задаваемой функцией потерь , то статистическая игра имеет значение (цену) :

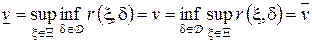
и существуют оптимальные (или 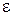-оптимальные) стратегии обоих игроков.

Дата добавления: 2015-06-27