Упражнения. 1. Используя известные из общего курса теории игр методы решения матричных игр и (см

1. Используя известные из общего курса теории игр методы решения матричных игр 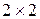и 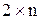(см. например [2]), решите задачу, поставленную в иллюстративном примере п.1.3:

а) Найдите оптимальные стратегии первого и второго игроков в исходной антагонистической игре 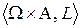и значение этой игры .

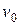б) Найдите минимаксное решающее правило , наименее благоприятное априорное распределение 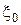и значение игры v в статистической игре 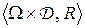; поясните содержательный смысл различия между 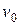и v.

в) Используя решение упражнения п.2.2, постройте минимаксное ре­шающее правило поведения 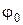, эквивалентное по риску найденному в (б) минимаксному рандомизированному решающему правилу .

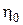г) Пусть по многолетним наблюдениям известно, что в летние дни погода бывает хорошей в 75% случаев; найдите байесовское решающее правило 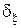относительно соответствующего априорного распре­деления 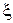. Опишите множество априорных распределений 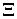в рассматриваемой задаче, постройте график минимального байесовского риска 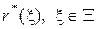, и интерпретируйте результат, полученный в (б).

2. Пусть в условиях задачи, решённой в упр. 1, наблюдение случайной величины X (получение прогноза погоды) стоит 0,2 ед. Затратив 0,4 ед., можно получить прогноз с вероятностью правильного предсказания, равной 0,9 как для плохой, так и для хорошей погоды. Какой из видов прогноза следует предпочесть?

3.2. Геометрическая интерпретация статистической игры при конечном множестве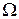

Если множество состояний природы конечно, 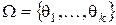, то каждому решающему правилу 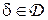можно поставить в соответствие 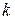-век­тор риска 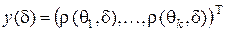. Множеством рисков в статистической игре называется разбиение

.

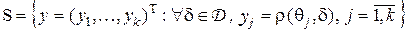Множество рисков 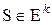является выпуклой оболочкой множества нерандомизированных рисков

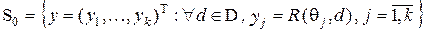
и описывает статистическую игру с конечным 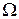с точностью до эквивалентных решающих правил. Крайние точки выпуклого множества S соответствуют нерандомизированным решающим правилам.

Для конечного 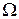любое априорное распределение может быть представлено в виде 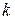-вектора

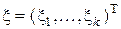с .

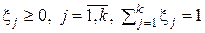Байесовский риск любого правила 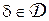относительно априорного распре­деления 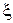равен

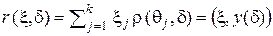
и одинаков для всех точек гиперплоскости 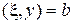. Байесовскому правилу 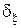соответствует 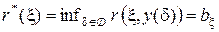. Поэтому все байесовские решающие правила относительно заданного 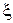могут быть представлены точками границы выпуклого множества рисков S, общими с опорной гиперплоскостью 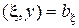. Величина минимального байесовского риска 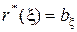определяется координатами точки пересечения этой опорной гиперплоскости с прямой 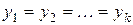(см. рис. 1).

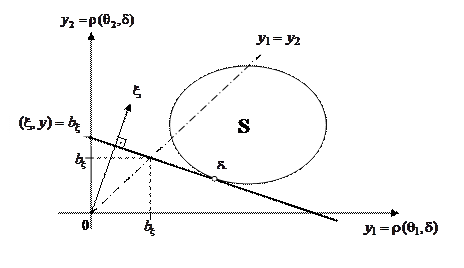
Рис. 1

Из этой геометрической интерпретации следует, что для любого байесовского решающего правила 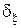относительно заданного 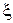существует хотя бы одно эквивалентное нерандомизированное байесовское правило 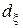(крайняя точка множества рисков S) относительно того же .

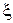Точки пересечения границы множества

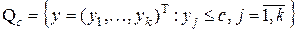
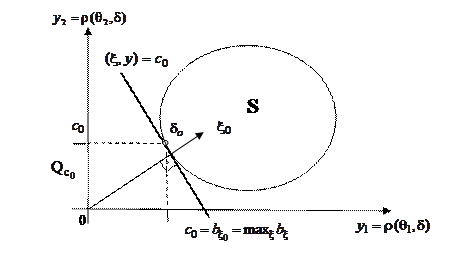
с множеством рисков S соответствуют решающим правилам , эквивалентным по максимальному риску 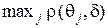. Поэтому минимаксные решающие правила найдутся как точки пересечения множества рисков S с наименьшим множеством 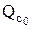, для которого 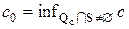(см. рис. 2).

Рис. 2

Величина 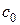есть значение статистической игры (минимаксный риск) v. Из этой геометрической интерпретации следует, что минимаксное решающее правило , если оно существует, совпадает с байесовским решающим правилом 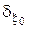относительно наименее благоприятного априорного распределения 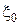, причём 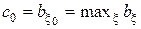, и что может не существовать нерандомизированное решающее правило (точка может не являться крайней точкой выпуклого множества S).

Дата добавления: 2015-06-27