Основные понятия теории антагонистических игр

Итак, теория игр есть теория математических (формальных) моделей принятия решений в условиях конфликта (см., например [2, 7, 8]).

Это – сравнительно молодой раздел математики и история теории игр, по существу, началась с работ фон Неймана и Моргенштерна в 1944 г. Сейчас теоретико-игровые методы находят широкое практическое применение в различных областях – от техники и экономики до медицины.

Классификация игровых моделей, рассматриваемых современной теорией игр, весьма разнообразна. Наиболее разработанной является теория антагонистических игр: два игрока выбирают независимо друг от друга свои стратегии (возможные действия), после чего игрок I получает от игрока II некоторый выигрыш, зависящий от пары выбранных стратегий (от ситуации).

Антагонистической игрой называется система:

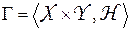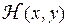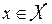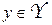c , , , (1)

где X, Y – множества стратегий I и II игроков, соответственно;

– функция выигрыша игрока I (то есть функция потерь игрока II).

Это – так называемая нормальная форма игры.

Естественный принцип оптимальности для антагонистической игры – принцип максимина (минимакса). Оптимальные стратегии 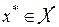, 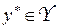соответствуют седловым точкам функции выигрыша :

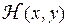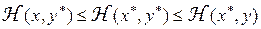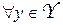для , . (2)

Таким образом, решение игры (седловая точка 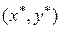) соответствует ситуации равновесия, отклонение от которой невыгодно для любого игрока.

Теорема 1. Для того, чтобы функция выигрыша 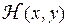имела седловые точки на 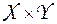, необходимо и достаточно, чтобы выполнялось равенство минимаксов

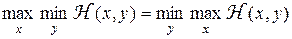, (3)

где внешние экстремумы достигаются на седловой точке .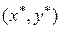

Заметим, что для 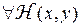, определённой на 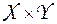, имеет место неравенство

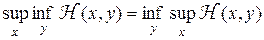(4)

Даже в простейших случаях функция выигрыша 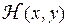может не иметь седловых точек и принцип максимина оказывается нереализуемым. Тогда можно использовать смешанное расширение игры . Если , 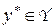это чистые стратегии игроков, то смешанные стратегии - это вероятностные меры (распределения вероятностей) 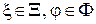, заданные на 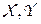, соответственно.

Теперь вместо 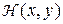рассматривается математическое ожидание

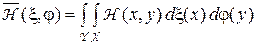(5)

и мы получаем расширенную игру:

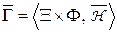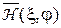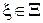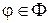c , , . (6)

Если имеет место равенство

, (7)

то общее значение этих смешанных экстремумов называют значением (ценой) игры 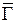. Если в (7) внешние экстремумы достигаются, то

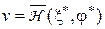, (8)

где 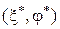- седловая точка функции выигрыша 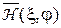. При выполнении (7) принцип максимина называется реализуемым.

Если в (7) внешние экстремумы не достигаются, то при 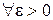существует 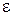-седловая точка 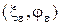такая, что

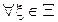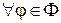для , . (9)

В современной теории антагонистических игр показано, что при достаточно слабых условиях на 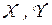, 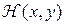расширенная игра 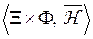имеет значение и существуют оптимальные (или 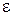-оптимальные) решения в смешанных стратегиях (теоремы о минимаксах).

Если в антагонистической игре каждый игрок располагает конечным множеством чистых стратегий, то мы имеем матричную игру (m 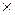n) с матрицей выигрыша I-го игрока A:

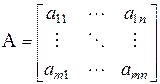. (10)

Смешанные стратегии здесь – вектора:

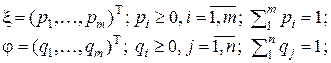(11)

Математическое ожидание функции выигрыша I-го игрока теперь равно

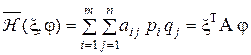. (12)

Для любой матричной игры справедлива теорема о минимаксах.

Теорема 2. Какова бы ни была матрица игры A, имеют место равенства

, (13)

или, что эквивалентно – существует седловая точка :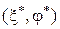

. (14)

Дата добавления: 2015-06-27