Принцип доминирования по Парето

Этот принцип применяется в моделях принятия решений по нескольким критериям.

Пусть альтернативы а₁, а₂,… а_n оцениваются по нескольким (двум) критериям: К₁ и К₂.

Если альтернатива a_i равносильна альтернативе a_j по критерию К₁, то

a_i ~¹ a_j

Если альтернатива a_i равносильна альтернативе a_j по критерию К₂, то

a_i ~² a_j

Если альтернатива a_i предпочтительнее альтернативы a_j по критерию К₁, то

Если альтернатива a_i предпочтительнее альтернативы a_j по критерию К₂, то

Если альтернатива a_i не хуже альтернативы a_j по критерию К₁, то

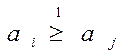
Если альтернатива a_i не хуже альтернативы a_j по критерию К₂, то

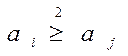
Пусть a_i ~¹ a_j и

Следовательно, a_i доминирует по Парето альтернативу a_j

Пусть a_i ~² a_j и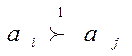

Следовательно, a_i доминирует по Парето альтернативу a_j

В общем случае принцип доминирования по Парето является способом попарного сравнения всех альтернатив. Логически возможны следующие случаи:

1. по всем критериям альтернативы a_i и a_j эквивалентны, тогда альтернативы a_i и a_j эквивалентны с точки зрения принятия решений

2. по одним критериям альтернативы a_i и a_j эквивалентны, а по другим a_i предпочтительнее альтернативы a_j, тогда a_i доминирует по Парето альтернативу a_j

3. по одним критериям a_i предпочтительнее альтернативы a_j, а по другим – a_i хуже альтернативы a_j, тогда альтернативы a_i и a_j несопоставимы по Парето.

Пример:

Инвестор должен выбрать один из альтернативных способов размещения активов.

Каждый способ (альтернатива) определяется средним ожидаемым доходом (m_i) и риском – средним квадратичным отклонением (σ_i), где i – номер альтернативы.

Требуется отбросить заведомо плохие альтернативы и составить множество для выбора.

Решение:

риск А₅

А₃ А₄

А₂

А₁

Ожидаемый доход

Рис.1 «Доминирование по Парето в задаче принятия решения с риском»

А_i(m_i, σ_i)

Сравниваем альтернативы попарно.

Сравним А₁ и А₂

Имеем: А₁~^mА₂ А₁>^σА₂, так как σ₁>σ₂

Следовательно А₂ – доминируемая стратегия и её можно исключить

Аналогично сравниваем остальные стратегии и получаем, что стратегия А₃ – доминируемая, следовательно её тоже отбрасываем

Мы отбросили стратегии А₂ и А₃ – доминируемые. Инвестор может выбирать из альтернатив А₁, А₄, А₅.

Итак, принцип доминирования по Парето позволяет отбросить доминируемые альтернативы и оставить для рассмотрения множество по Парето несопоставимых альтернатив, называемые альтернативами эффективными по Парето.

Таким образом, принцип доминирования по Парето облегчает задачу принятия решения. Для задачи выбора альтернативы по двум критериям средний ожидаемый доход (m_i) и риск r_i множество альтернатив, эффективных по Парето, будет лежать на кривой с положительным наклоном:

риск

А₃

А₂

А₁

Ожидаемый доход

Рис. 2 «Альтернативы эффективные по Парето»

Дата добавления: 2015-06-27