Постановка проблемы. Оптимальные решения в условиях риска

Оптимальные решения в условиях риска

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Microsoft Windows. Руководство пользователя. М.: АО Диалог. 1997.

2. Берлинер Э.М., Глазырин Б.Э., Глазырина И.Б. Microsoft Office 97 Русская версия. М. ABF, 1997.

3. Йенсен К., Вирт Н. Паскаль. Руководство для пользователя. -М.: Финансы и статистика, 1989.

4. В. Пасько. Word 97. – К.: BHV, 1997.

5. Дж. Уокенбах. Excel 97. Библия пользователя. – К., Диалектика, 1997.

7. П. Бернс, Дж. Николсон Секреты Excel 97 для Windows 98. – К., Диалектика. 1997.

8. Word 97 для Windows в примерах. BHV: Санкт-Питербург, 1997

Задача принятия решения при риске отличается от задачи принятия решения при неопределенности тем, что в первом случае лицо, принимающее решение (ЛПР) имеет определенную информацию о вероятностях различных состояний среды. Поскольку риском называется оцененная любым способом вероятность, то ситуации принятия решения с вероятностными оценками – это ситуации принятия решения в условиях риска.

Информированность ЛПР о вероятностях состояния среды может быть различна. Например, ЛПР знает только, что один состояния более вероятны, чем другие, или ЛПР знает, что вероятность какого-то состояния меньше 50%. Максимально информированный ЛПР знает вероятности различных состояний среды.

Предположим, что ЛПР стремится максимизировать некую целевую функцию, которую мы обозначим X. Например, прибыль, доход и т. д.

Предположим, что ЛПР может выбрать одну из альтернатив: А₁, А₂, А₃,…А_n. Каждой альтернативе при этом соответствует определенное управленческое решение.

Пусть значение целевой функции X зависит как от выбора альтернативы А_i, так и от случайных факторов, зависящих от состояния окружающей среды.

При этих допущениях целевая функция X будет определяться как набор случайных величин X₁, X₂, X₃,…, X_n, где

X₁ – случайная величина, характеризующаяся распределением вероятностей при выборе альтернативы А₁

X₂ – случайная величина, характеризующаяся распределением вероятностей при выборе альтернативы А₂

…

X_n – случайная величина, характеризующаяся распределением вероятностей при выборе альтернативы А_n

Пример:

У человека есть 100 рублей. Он стоит перед выбором: купить лотерейный билет с выигрышем 1000 рублей с вероятностью 0,4, купить лотерейный билет с выигрышем 500 рублей с вероятностью 0,7, либо оставить 100 рублей в располагаемый доход.

Решение:

Представим ситуации виде задачи принятия решения с рисками.

А₁, А₂, А₃ ­– решения-альтернативы

X – доход

X = выигрыш – 100 (при А₁ и А₂)

X = 100 (при А₃)

Если ЛПР выберет А₁, то

X₁ = 1000–100=900

Если ЛПР выберет А₂, то

X₂ = 500–100=400

Если ЛПР выберет А₃, то

X₃ = 100

Выигрыши и вероятности представим в виде таблицы:

	А1	А2	А3
Вероятность (р)	0,4	0,6	0,7	0,3
Выигрыш (X)		-100		-100

2. Математическое ожидание – оценка доходности

Каждая случайная величина X_i с известным законом распределения вероятностей характеризуется определенным набором констант, называющихся числовыми характеристиками.

Первая такая характеристика – математическое ожидание М(X)

Для дискретных случайных величин математическое ожидание равно:

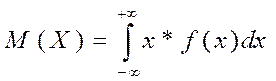(1)

Математическое ожидание определяет среднее, взвешенное по вероятностям, значение случайной величины X:

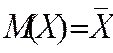(2)

Для нашего примера рассчитаем математические ожидания:

М(X₁)=0,4*900+0,6*(-100)=300 рублей

М(X₂)=0,7*400+0,3*(-100)=250 рублей

М(X₃)=100 рублей

С точки зрения ожидаемого дохода альтернатива А₁ лучше альтернативы А₂, которая в свою очередь лучше, чем альтернатива А₃.

Но при этом не учитывался риск.

Для учета риска применяются такие характеристики как дисперсия и среднее квадратичное отклонение.

Дата добавления: 2015-06-27