Принятие решений в условиях риска по интегральному критерию

Задача принятия решения с риском содержит A_i, оцененную по m_i – средний ожидаемый доход, σ_i – риск.

Пусть применим принцип доминирования по Парето и получим множество альтернатив эффективности по Парето:

σ_i

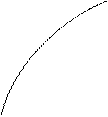А₃

А₂

А₁

m_i

рис. 3

Необходимо выбрать наилучшую альтернативу из множества на рисунке 3.

Для этого применяется интегральный (агрегированный) критерий. В общем случае, если альтернативы оцениваются по двум критериям: К1 и К2.

Интегральный критерий – это функция двух переменных:

f(K₁,K₂)

Возможны различные варианты вида функции.

Например, f(K₁,K₂)=К₁^α*К₂^(1–α) или f(K₁,K₂)=α*К₁+β*К₂

α–значимость критерия К₁

β– значимость критерия К₂

Естественно требование удовлетворения интегрального критерия следующим свойствам:

- Если альтернативы a_i и a_j эквивалентны по всем критериям, то значения интегрального критерия для этих альтернатив равны (и наоборот)

- Если a_i доминирует по Парето альтернативу a_j, то значение интегрального критерия для a_i больше соответствующего значения для а_j (и наоборот)

Составим линейный интегральный критерий для случая, когда первый критерий – средний ожидаемый доход, а второй – риск:

f(m, σ) = α*m – β* σ

m – средний ожидаемый доход

σ – риск

α≥0 и β ≥0

Пусть α >0, следовательно, агент принимает во внимание ожидаемый доход

Тогда имеем при делении на α:

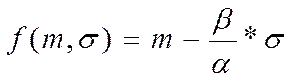
λ = β / α >0

Или

f(m, σ) = m – λ * σ,

λ = const≥0

Раскроем смысл постоянной величины λ.

Если для ЛПР значение λ равно нулю (λ =0), тогда f(m, σ) = m.

Это значит, что субъекта интересует только доход.

Это нейтральность к риску ЛПР.

Если есть два экономических субъекта, таких, что:

Для первого: f₁(m, σ) = m – σ, то есть λ₁ =1

Для второго: f₂(m, σ) = m – 2*σ, то есть λ₂ =2

Можно сделать вывод, что второй субъект более чувствителен к риску.

Если предположить, что f(m, σ) = m + σ

Это означает, что данный экономический агент склонен к риску

Таки образом λ отражает отношение ЛПР к риску:

λ =0 ® нейтральность

λ <0 ® склонность к риску

Чем больше λ, тем чувствительнее субъект к риску

Пример:

Для ЛПР λ=3.

Оценить с помощью неравенства Чебышева его гарантированную вероятность, на которую ориентируется ЛПР.

Решение:

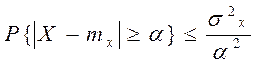
ЛПР имеет отклонение X от M(X) на величину больше, чем α.

f(m, σ) = m – 3* σ, следовательно неприятности начинаются при

α. = 3* σ

Имеем,

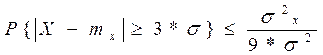
Вероятность неприятностей должна быть не больше 1/9. Следовательно данный ЛПР выбирает гарантированную вероятность равную 8/9.

Заметим, что мы действовали как вольные интерпретаторы, то есть полученное решение не строго математическое.

Дата добавления: 2015-06-27