
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ограничения применения Д.А
|
|
|
|
Виды ДА.
Виды переменных в ДА.
Переменные в ДА принято делить на два вида – независимые и зависимые. Независимой переменной (фактором) называется контролируемая экспериментатором переменная. В качестве независимых переменных могут выступать психологические, экономические и другие переменные, такие как уровень развития интеллекта, свойства темперамента или характера, показатели эффективности, качество оборудования, пол испытуемых, возраст, национальность, производительность, принадлежность к какой-либо социальной группе и т.д., т.е. по каким именно различиям между испытуемыми будут сформированы экспериментальные группы. Независимой переменной могут быть действия других людей, которым подвергаются испытуемые или условия проведения эксперимента.
Независимую переменную принято делить на уровни, которые могут различаться как количественно, так и качественно. Уровнями независимой переменной могут быть, например, уровень мотивации испытуемых (высокий, средний, низкий), уровень заработной платы и ее влияние на результативность деятельности и т.д., которые различаются лишь количественно. Уровни независимой переменной представляют собой не только градации какого-либо фактора, но и характеристики, различающиеся, прежде всего, качественно. Например, цвет глаз, виды заболеваний, виды рекламы и т.д. В таком случае их правильнее всего будет называть условиями действия фактора или условиями эксперимента.
Зависимой переменной называется переменная, которая при ее измерении во время эксперимента подвергается влиянию независимой, например, возраст испытуемых может влиять на производительность труда (зависимая переменная), уровень интеллекта на скорость решения творческих задач, социальное положение на ценностные ориентации и т.д.
ДА принято делить на несколько видов согласно количеству независимых переменных: однофакторный ДА (одна независимая переменная), двухфакторный ДА (две независимых переменных), трехфакторный ДА (три независимых переменных) и мультифакторный Д.А.(более трех независимых переменных). Обычно исследоваия ограничиваются применением только двух первых видов ДА, поскольку уже в трехфакторном ДА вычисления являются довольно громоздкими и часто требуют большого эмпирического материала, но во всех видах ДА независимая переменная только одна.
ДА можно применять только в том случае, когда переменная измерена в шкале интервалов или отношений, т.е. когда можно вычислить основные параметры распределения (средние и дисперсии). Кроме того, должно быть либо известно, либо доказано, что зависимая переменная распределена по нормальному закону (в противном случае полученные выводы могут оказаться ложными).
Проверка нормальности распределения результативного признака.
Нормальность распределения результативного признака можно проверить тремя способами:
1) Путем расчета показателей асимметрии и экцесса и сопоставления их с критическими значениями.
2) С помощью коэффициента вариации.
3) С помощью критерия  .
.
Перейдем к более детальному изучению каждого из предложенных способов на конкретных примерах.
Пример 1 (взят Е. Сидоренко)
В выборке курсантов военного училища (юноши в возрасте от 18 до 20 лет) измерялась способность к удержанию физического волевого усилия на динамометре. В первый день эксперимента у них, наряду с другими показателями измерялась мышечная сила каждой из рук. На второй день эксперимента им предлагалось выдерживать на динамометре мышечное усилие, равное ½ максимальной мышечной силы данной руки. На третий день эксперимента испытуемым предлагалось проделать то же самое в парном соревновании на глазах у всей группы. Пары соревнующихся были подобраны таким образом, чтобы силы обеих рук у них примерно совпадала. Результаты представлены в таблице 2. Можно ли считать, что фактор соревнования в группе каким-то образом влияет на продолжительность удержания усилия. Подтверждается ли предположение о том, что правая рука более социальна.
Таблица 1. Длительность удержания усилия (сек/10) на динамометре правой и левой руками в разных условиях измерения (n=4).
| Код имени испытуемого | Наедине с эксперимент. (А  ) )
| В группе (А 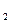 ) )
| ||
| Правая рука | Левая рука | Правая рука | Левая рука | |
| 1. Л-в | ||||
| 2. С-с | ||||
| 3. С-в | ||||
| 4. К-в |
Таблица 2. Вычисление показателей асимметрии и экцесса, коэффициента вариации по показателю длительности попыток решения анаграмм.
| N | 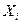
| (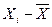 ) )
| (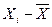 ) ) 
| (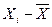 ) ) 
| (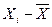 ) ) 
|
| 0,94 2,94 1,94 -1,06 | 0,884 8,644 3,764 1,124 | 0,831 25,412 7,301 -1,191 | 0,781 74,712 14,165 1,262 | ||
| -1,06 0,94 -2,06 -0,06 | 0,004 0,884 4,244 0,004 | -0,000 0,831 -8,742 -0,000 | 0,000 0,781 18,009 0,0000 | ||
| 4,94 3,94 -2,06 -3,06 | 24,404 15,524 4,244 9,304 | 120,554 61,163 -8,742 -28,653 | 595,336 240,982 18,009 87,677 | ||
| -0,06 -0,06 -5,06 -2,06 | 0,004 0,004 25,604 4,244 | -0,000 -0,000 -129,554 -8,742 | 0,000 0,000 655,544 18,009 | ||
| Сумма | 102,944 | 30,468 | 1725,467 |
Для расчетов в таблице 4 сначала необходимо определить среднюю арифметическую по формуле:  , где
, где  - каждое наблюдаемое значение признака; n – количество наблюдений. В данном случае
- каждое наблюдаемое значение признака; n – количество наблюдений. В данном случае 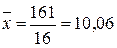 . Среднее квадратическое отклонение вычисляется по формуле:
. Среднее квадратическое отклонение вычисляется по формуле: 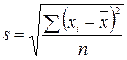 . В данном случае
. В данном случае  .
.
Показатели асимметрии и экцесса с 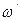 ошибками репрезентативности определяются по следующим формулам:
ошибками репрезентативности определяются по следующим формулам:
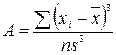 ,
,  ;
; 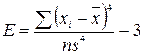 ,
, 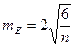 .
.
В данном случае  ,
,  ;
;
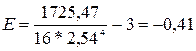 ,
, 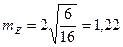 .
.
Заметим, что показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирического распределениях от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз, т.е.  ,
,  .
.
В данном случае 
 . Мы видим, что оба показателя не превышают в три раза свою ошибку репрезентативности, следовательно, распределение данного признака не отличается от нормального. Теперь произведем проверку по формулам Е.И. Пустыльника. Рассчитаем критические значения для показателей А и Е.
. Мы видим, что оба показателя не превышают в три раза свою ошибку репрезентативности, следовательно, распределение данного признака не отличается от нормального. Теперь произведем проверку по формулам Е.И. Пустыльника. Рассчитаем критические значения для показателей А и Е.
 ,
,  , где n – количество наблюдений
, где n – количество наблюдений
В данном случае:  ;
;

Аэмп=0,106, Аэмп<Акр; Еэмп=-0,711, Еэмп<Екр. Итак, оба варианта проверки по Н.А. Плохинскому и по Е.И. Пустыльнику подтверждают, что результативный признак нормально распределен.
Второй способ проверки – вычисление коэффициента 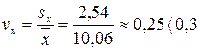 , следовательно, по нашим данным распределение результативного признака – нормальное.
, следовательно, по нашим данным распределение результативного признака – нормальное.
Третий способ проверки. Покажем на данном примере применение критерия 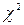 для определения «нормальности» распределения. Разобьем данные на интервалы. Число интервалов вычислим с помощью формулы Стердесса
для определения «нормальности» распределения. Разобьем данные на интервалы. Число интервалов вычислим с помощью формулы Стердесса 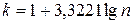 . В нашем случае
. В нашем случае 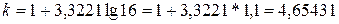
Округляем  до целого(заметим, всегда в сторону увеличения),
до целого(заметим, всегда в сторону увеличения),  . Находим длину интервала
. Находим длину интервала 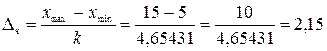 . Строим таблицу распределения частот по интервалам.
. Строим таблицу распределения частот по интервалам.
Таблица 3. Таблица распределения частот по интервалам.

| 4,95-7,1 | 7,1-9,25 | 9,25-11,4 | 11,4-13,55 | 13,55-15,7 |
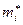
| |||||
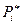
| 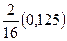
| 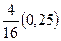
| 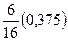
| 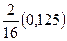
| 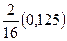
|
Вычислим теоретическую вероятность попадания случайной величины Х, распределенной по нормальному закону, в рассматриваемые интервалы
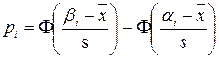 .
.
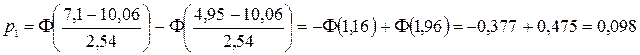

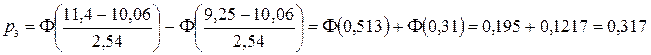

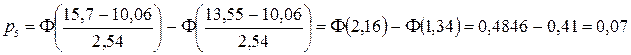 Составляем таблицу распределения эмпирических и теоретических частот по интервалам для применения критерия
Составляем таблицу распределения эмпирических и теоретических частот по интервалам для применения критерия 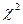 .
.
Таблица 4. Таблица распределения эмпирических и теоретических частот по интервалам.

| 4,95-7,1 | 7,1-9,25 | 9,25-11,4 | 11,4-13,55 | 13,55-15,7 |
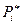
| 0,125 | 0,25 | 0,375 | 0,125 | 0,125 |
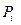
| 0,098 | 0,255 | 0,375 | 0,215 | 0,07 |
Воспользовавшись формулой,  , получаем
, получаем  Итак,
Итак, 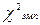 =0,16. Определяем
=0,16. Определяем  , где ע (число степеней свободы)=
, где ע (число степеней свободы)=  =16-5-2=9,
=16-5-2=9,  =16,919. В силу того, что 0,16<16,919
=16,919. В силу того, что 0,16<16,919  то по критерию
то по критерию 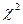 распределение подчиняется нормальному закону.
распределение подчиняется нормальному закону.
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!