Искусственный нейрон

ЛАБОРАТОРНАЯ РАБОТА № 15. НЕЙРОННЫЕ СЕТИ. ПЕРСЕПТРОН.

Искусственный нейрон (рис.1) имитирует в первом приближении свойства биологического нейрона.

На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, и все произведения суммируются, определяя уровень активации нейрона.

Рис.1 Модель искусственного нейрона

Множество входных сигналов, обозначенных x₁,x₂,…x_n, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаются вектором X, Каждый сигнал умножается на соответствующий вес w₁,w₂,…w_n, и поступает на суммирующий блок, обозначенный Σ. Множество весов в совокупности обозначается вектором W. Суммирующий блок, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть . В векторных обозначениях это может быть компактно записано следующим образом:

Сигнал NET далее, как правило, преобразуется функцией активации F и дает выходной нейронный сигнал OUT. Возможны совершенно различные функции активации. Но чаще всего используются (см. рис.2):

1) обычная линейная функция OUT=k(NET), где k— константа, величина которой меняет наклон функции.

2) пороговая функция, где k- величина порога, изменение которой сдвигает порог,

3) логистическая функция

На рис.2 приведены основные активизационные функции нейронов и способы их формирования в Маткаде.

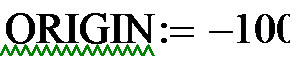
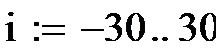
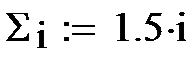
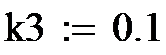
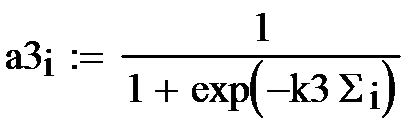
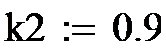
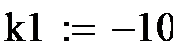
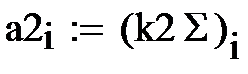
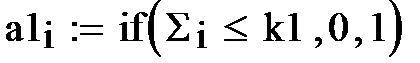
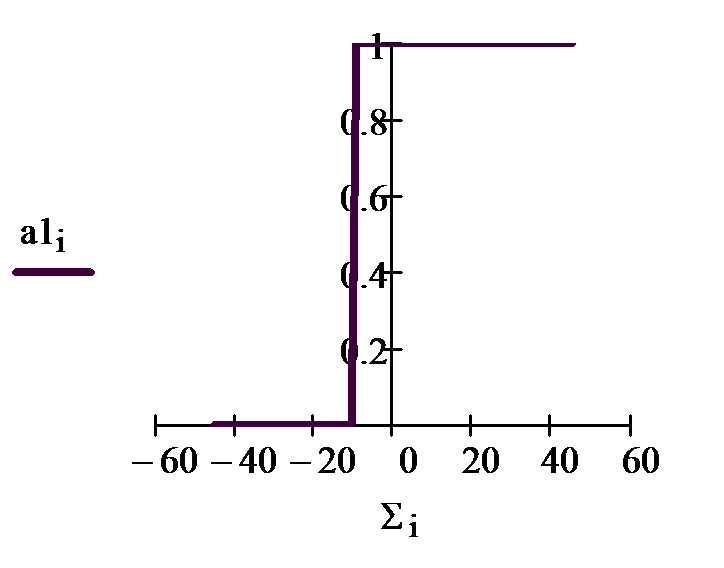
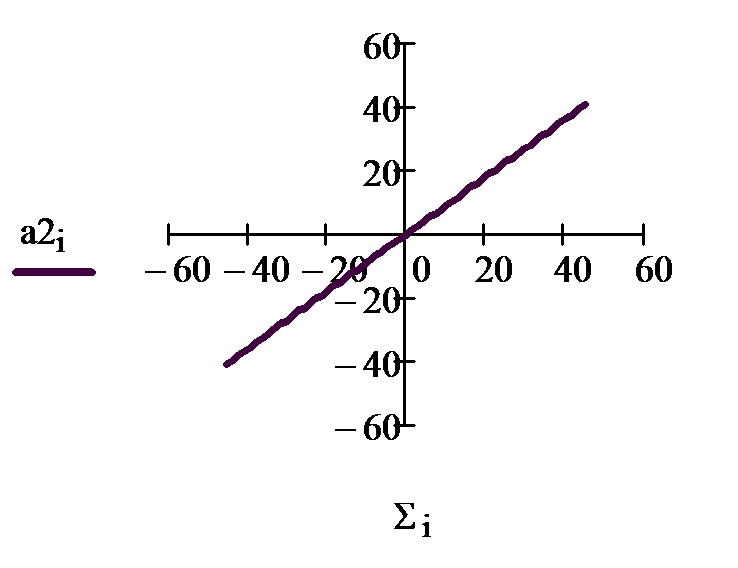
Рис.2. Основные функции активации и их реализация в Маткаде.

Так как наши графики захватывают третий и четвертый квадранты, то счет мы начинаем от -100 (ORIGIN:= -100).

Логистическая функция используется наиболее часто, т. к. она обладает свойством дифференцируемости, что нужно при обучении нейрона, и имеет переменный коэффициент усиления: при малых значениях аргумента он большой, а при увеличении аргумента – уменьшается. Изменение коэффициента k изменяет крутизну логистической функции.

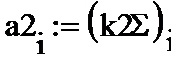Задание1. Студент сначала должен разобраться в приведенных выражениях, а затем набрать каждую функцию в Маткаде по очереди

А). Для пороговой функции следует рассмотреть ее работу при значениях порога к1= 0 и +15.

Б). Работу линейной функции следует проверить при значениях коэффициента к2= 5 и -1;

В). Вид логистической активизационной функции нужно рассмотреть при значениях коэффициента к3 = 0.1, 1.5 и 3.

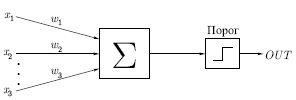Персептрон.

Нейрон или нейронная сеть, с пороговыми функциями активации называется персептроном. (Рис.3). Это одна из самых простых нейронных моделей. Она разработана в 60-х гг. прошлого века Розенблаттом.

Рис.3 Персептрон на три входа.

На входы персептрона подаются входные сигналы. Элемент умножает каждый вход на вес и суммирует взвешенные входы. Если полученная сумма больше заданного порогового значения, выход равен единице, в противном случае - нулю.

А). Обучение персептрона. Персептрон способен к обучению. Сеть обучается, чтобы для некоторого множества входов давать желаемое множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.

Различают алгоритмы обучения с учителем и без учителя. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть, и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, ошибки вычисляются и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Персептронможет быть обучен не всему. Некоторым функциям, например, исключающему ИЛИ, его обучить нельзя. Функции, которым можно обучить персептрон, называются линейно разделимыми. Их определение составляет нетривиальную задачу. В этом ограниченность персептрона.

Предложенный Ф. Розенблаттом метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает несколько шагов:

Шаг0: Для заданных входов задается желаемый выход. Начальные значения весов всех нейронов представляются случайными.

Шаг1: Вычисляется вектор ошибки δ между заданным и полученным значением выхода.

Шаг2: Вектор весов модифицируется по формуле . Здесь W_i и W_i+1 –Векторы весов до и после очередной итерации, Х- вектор входных сигналов, δ^Т- транспонированный вектор ошибки, 1<η<1 – темп обучения.

Шаг3: Шаги 1 -2 повторяются до тех пор, пока вектор ошибки не станет достаточно малым.

На рис.4 приведена Маткад- программа обучения персептрона из одного нейрона с двумя входами.

1. Задаются порог к, случайные значения входов х01 и х02, желаемое значение выхода у0=1 и нулевые начальные значения весов w.

2. Составляется программа обучения. Задается начальное значение ошибки D=2 и в цикле с оператором while D>0 подсчитываются сумма Σ, фактическое значение и выхода у.

3. Подсчитывается ошибка D = y0 – y и новое значение весов с коэффициентом обучения η =1.

4. 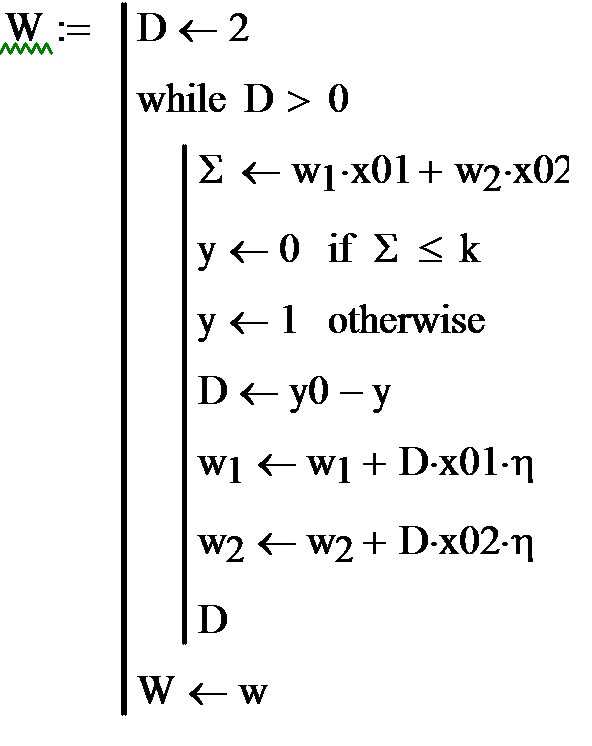Цикл продолжается пока D>0. В результате получаем значение вектора W, удовлетворяющее требуемой величине ошибки.

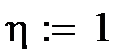
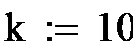
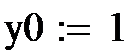
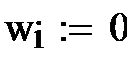
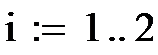
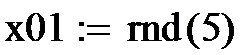
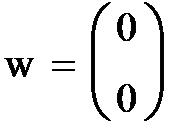
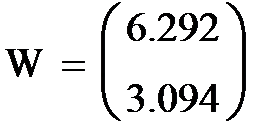
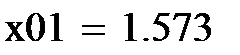
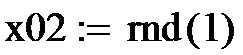
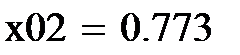
Рис.4 Программа обучения персептрона.

Убедимся, что при полученных значениях весов, выход персептрона равен 1.Для этого составим небольшую программу, приведенную на рис.5.

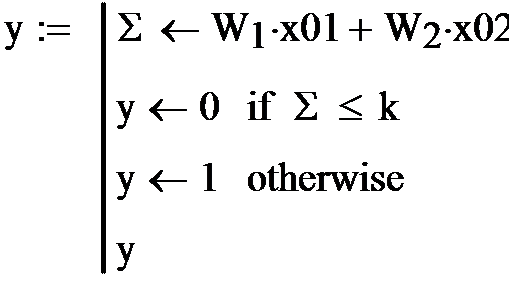
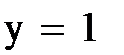
Рис.5.Проверка вычисленных весов.

Из программы видно, что при подаче заданных входных сигналов выход равен 1.

Б).Обученный персептрон разделяет входные сигналы на два класса.

Если на вход персептрона подать входные сигналы, то, в зависимости от знака Σ выход будет равен 0 или 1. Тем самым входные сигналы делятся на два класса. Так как в векторной форме , то выражение Σ=0 является границей этих двух классов.

На рис. 6 приведена программа классификации десяти точек. Случайным образом сформированы десять входных сигналов. Для подсчитанных выше весов из условия Σ=0 граница. Все входные сигналы располагаются выше или ниже этой границы в зависисти от того, равен соответствующий им выход един единице или нулю.

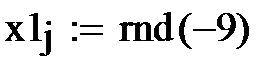
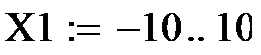
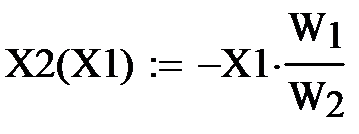
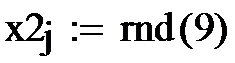
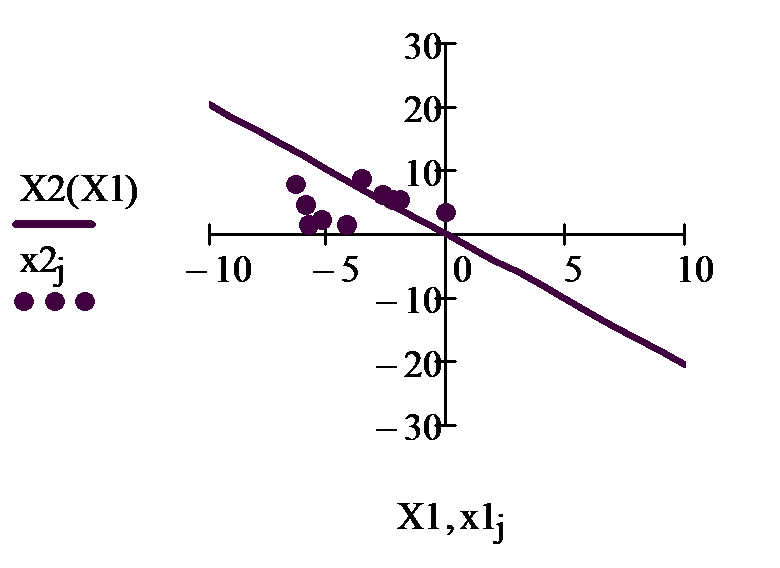
Рис.7. Разделение входных сигналов персептрона на два класса

ЗАДАНИЕ 2. Студент должен разобраться в программах, набрать их в Маткаде и проиграть их несколько раз.

Дата добавления: 2015-06-27