Двухуровневые планы многофакторных экспериментов

В многофакторном эксперименте можно учитывать только зависимость выхода от каждого из факторов, а

можно учитывать также зависимость выхода от взаимодействия нескольких факторов. Если учитывается взаимодействие всех факторов, то многофакторный эксперимент.называется полным.

Самым простым планом многофакторного полного эксперимент является план, в котором исследуемые факторы изменяются лишь на двух уровнях: верхнем C_i⁺ и нижнем C_i^-. Такой план называется двухуровневым и обозначается ПФЭ2ⁿ, т.е. полный факторный эксперимент двухуровневый, n- факторный.

Центр эксперимента,

интервал варьирования

В безразмерном выражении верхний уровень фактора будет выражаться +1, нижний _1:

План ПФЭ2ⁿ можно представить таблицей.

Пример. Построить план ПФЭ2² для исследования влияния температуры в диапазоне 30 – 42 градуса Цельсия и величины pH в диапазоне от 5 до 7.

Найдем центр эксперимента

И интервал варьирования

i	X1i	X2i	X1iX2i
	-	-	+
	-	+	-
	+	-	-
	+	+	+
Ci0
Λi

Здесь столбцы 2 – 3 отражают влияние отдельных факторов. Столбец 4 отражает межфакторное взаимодействие.

Заполнение второго и третьего столбца в пояснениях не нуждается. Четвертый столбец заполняется по правилу перемножения содержимого второго и третьего столбцов: Если второй и третий столбец имеют одинаковый знак, то в четвертом столбце ставится +, в противном случае -.

План полного двухфакторного эксперимента ПФЭ2² дает возможность вычислить четыре коэффициента уравнения регрессии:

План полного трехфакторного эксперимента дает возможность вычислить восемь коэффициентов уравнения регрессии

и т.д.

ЗАДАЧА. Методом наименьших квадратов рассчитать в Маткаде коэффициенты уравнения по результатам выполнения представленного в таблице полного двухуровневого трехфакторного плана ПФЭ 2³..

Рассчитывается восемь коэффициентов для уравнения:

I	Основные столбцы	Вспомогательные столбцы
X1i	X2i	X3i	X1iX2i	X2iX3i	X1iX3i	X1iX2iX3i	Y1i	Y2i	Y3i
	-	-	-	+	+	+	-
	-	+	-	-	-	+	+
	+	-	-	-	+	-	+
	+	+	-	+	-	-	-
	-	-	+	+	-	-	+
	-	+	+	-	+	-	-
	+	-	+	-	-	+	_
	+	+	+	+	+	+	+

Таблица 1

Здесь У – выход процесса. Произведено три повторности эксперимента.

1.В начале программы набираем 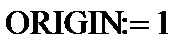, что означает, что счет всех элементов должен начинаться с единицы.

2. По таблице создаем матрицу выходов У и матрицу входов Х:

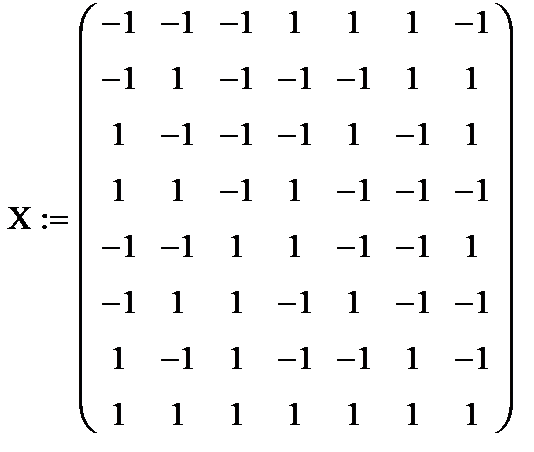
  3.Вычисляем среднее выходов:

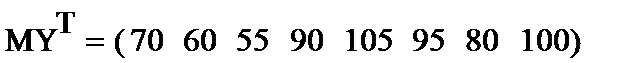
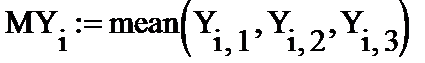
4. Задаем начальные приближения для коэффициентов:

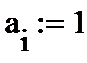
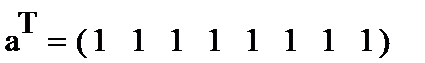
5.Введя оператор given, формируем вычислительный блок.

6.Набираем выражение для метода наименьших квадратов:

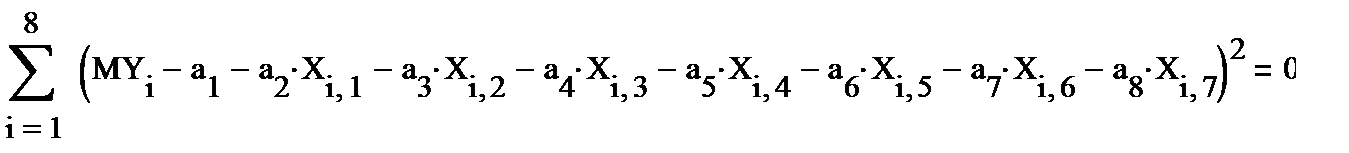
7. Решение ищем с помощью встроенной функции MINERR (Минимальная ошибка):

и получаем ответ

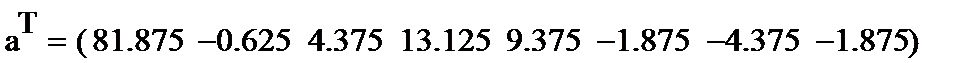
Записываем уравнение и сравниваем сначала визуально модель с объектом моделирования.

7.Вычисляем абсолютные W и относительные в процентах w ошибки модели

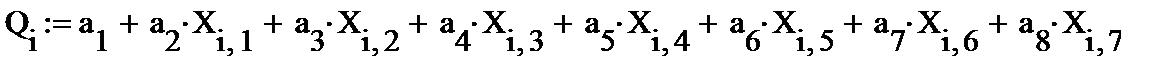
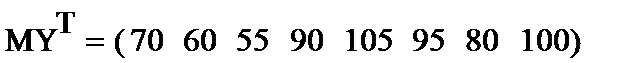
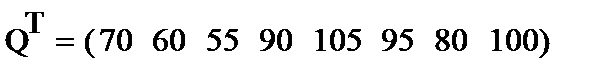
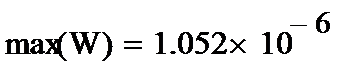
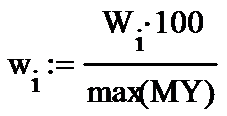
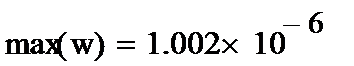
Проводим проверку значимости коэффициентов по Стьюденту:

Для этого:

8. вычисляем выборочную и дисперсию и с.к.о.

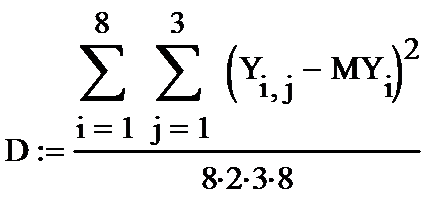
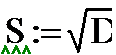
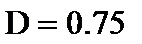
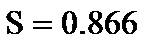
9. Вычисляем обратную функцию распределения Стьюдента для уровня значимости 0,95 и числа степеней свободы =16 Если в прямой функции распределения, задавшись значением случайной величины и числом степеней свободы, мы вычисляем вероятность, то в обратной функции, задавшись вероятностью и числом степеней свободы, мы получаем значение случайной величины.

Для Стьюдента, как известно, число степеней свободы равно удвоенному числу экспериментов.

10. Вычисляем доверительную ошибку ε и сравниваем ее с модулями значений коэффициентов.

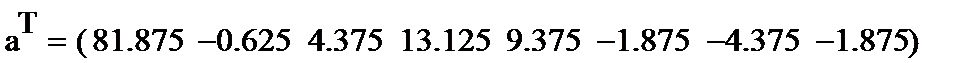
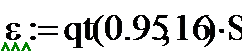
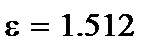
Мы видим, что второй коэффициент меньше доверительной ошибки, следовательно, он не значим.

11. Записываем уравнение регрессии без учета второго коэффициента:

Дата добавления: 2015-06-27