Лабораторная работа №18. Адаптивный фильтр Калмана

Проверка адекватности по Фишеру

12. Вычисляем функцию F.

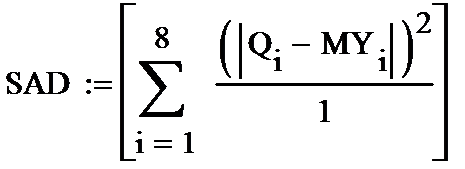
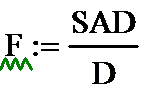
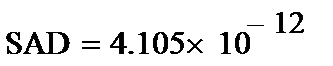
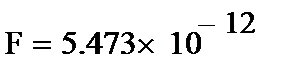
13. Вычисляем обратную функцию распределения Фишера:

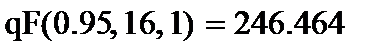
14. Так как Вычисленное F < qF, то с вероятностью 0,95 полученное уравнение адекватно экспериментальным данным.

Основной проблемой, возникающей при любых измерениях, является их недостаточная точность. Имеется два пути решения этой пробле­мы: повышение точности измерительных приборов и повышение точности путем статистической обработки избыточного числа измерений, в результате которой получают оценку измеряемой величины. Повышение точности измерительных приборов требует существенных затрат, в то время как статистическая обработка измерений при наличии компьютера стоит дешево и проводится достаточно быстро.

Сегодня существует множество методов статистической обработки измерений. Их можно разделить на два больших класса: просто статистической обработки и оптимальной обработки, в результате которой получают в каком- то смысле оптимальную оценку измеряемой величины. Кроме того, обычно разделяют методы статистической обработки для статических и динамических систем. Статистическая обработка статических систем изучалась на 4-м курсе. Это метод наименьших квадратов. Мы ниже рассмотрим несколько методов оптимальной статистической обработки информации динамических систем на конкретных примерах.

Сложность обработки информации в динамической системе заключается в том, что ее состояние меняется во времени и отдельные измерения переводить из одного состояния в другое.

Существует также несколько методов оптимальной статистической обработки для динамических систем. Это фильтры Винера, Винера- Хопфа и др.

В 1961 году американский математик КАЛМАН разработал оптимальный фильтр для линейных нестационарных систем. Преимуществом фильтра Калмана является то, что он решает задачу во временной, а не частотной области, как, например, фильтр Винера.

Калман разработал свой фильтр для многомерных задач Формулировка задачи, как правило, задается в матричной форме, однако мы рассмотрим ниже простейшие скалярные задачи. в матричной форме

Фильтр Калмана существует в непрерывной и в дискретных формах. Разберем дискретный фильтр Калмана.

Рассмотрим следующую задачу

Блок- схема исследуемого процесса имеет вид:

Ф(t)

Н(t)

z(t)

v(t)

w(t)

x(t)

y(t)

f(t)

Рис.1. Блок – схема объекта.

. Здесь Ф – линейный объект(т.е. объект описываемый линейными соотношениями), на выходе которого вырабатывается неслучайный сигнал y(t). На выходную величину воздействует аддитивный (в виде слагаемого) шум w(t). Шум w(t) – это какие –то случайности внутри нашей системы. После шума мы имеем выходную величину x(t). X(t) – выходной сигнал нашей системы есть сумма неслучайного процесса y(t) и шума. Поэтому это уже случайный процесс. Поэтому в целом наша система – вероятностная (стохастическая). Мы хотим определить неизвестный нам случайный выходной процесс y(t) измерить неслучайную выходную величину y(t), но измеряем мы не ее, и не случайный выходной сигнал системы x(t), а преобразованный линейным блоком Н случайный процесс z(t). Это так называемые косвенные измерения, когда меряется какая – то функция определяемой величины. В общем случае Ф и Н могут изменяться во времени.

Шумы W(t) и v(t) – нормально распределенные случайные процессы с нулевыми математическими ожиданиями,

M(v) =0 и с постоянными дисперсиями Q и R, соответственно.

Процесс x(t) также распределен нормально, т.к. любое линейное преобразование нормально распределенного процесса есть нормально распределенный случайный процесс, а шум w(t) подчиняется нормальному закону распределения. Измерения производятся с ошибкой v (t).

Таким образом, в действительности мы измеряем величину

, (1)

причем случайный процесс z (t) также распределен нормально.

Требуется построить фильтр, после которого мы получим наилучшую оценку величины y.

Каждое последующее состояние системы определяется предыдущим:

Нижеприведенная программа составлена для Q=R=0.1. Для оценки качества фильтрации в программе решается также уравнение незашумленного, якобы «неизвестного» нам процесса.

Программа решения данной задачи в Маткаде приведена на рис.2

Здесь: y-«незашумленная» переменная,

X1- оцениваемая переменная:

Z- измеряемая переменная.

В доцикловой части первым оператором присваивается начальное значение «незашумленной» и оцениваемой переменной, причем начальное значение оцениваемой переменной берется «с потолка», вводятся постоянные значения дисперсий обоих шумов и постоянной времени системы, производится первое измерение z и вычисляется первая оценка мат. ожидания и дисперсии.

Измерение рассматривается как сумма двух псевдослучайных величин, каждая из которых образуется с помощью двух функций:

Функция r n d (x) возвращает равномерно распределенное случайное число в диапазоне 0 –x.

Функция d n o r m (x,y,w) возвращает нормально распределенное псевдослучайное число для аргумента x, с математическим ожиданием y и с.к.о z.

В первой функции dnorm за мат. ожидание принято значение y – «незашумленной» переменной, во второй – мат. ожидание равно 0.

В цикловой части программы производится перевод оцениваемых переменной и дисперсии в новое состояние системы, затем переводится в новое состояние «незашумленная» пе

Рис.2. Программа фильтрации фильтром Калмана

ременная, производится новое измерение z и вычисляется новая оценка оцениваемой переменной и дисперсии. В последних операторах цикловой части производится накапливание измерений, оцениваемой и

«незашумленной» переменной в массивы, с целью вывода их на печать после окончания решения

На рис.3. приведены решение задачи. Кривая, изображенная штрихом – «незашумленная» переменная, непрерывная кривая – оценка, точечная кривая – измерения без фильтрации.

Рис.3. Графики кривых

Дата добавления: 2015-06-27