Присоединенная масса

Возмущение потока жидкости шаром изменяет (увеличивает) кинетическую энергию этого потока. Эффект увеличения кинетической энергии потока при обтекании им неподвижного шара легко рассчитывается с помощью полученных выражений для вектора скорости 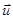. Для этого следует учесть, что полная скорость 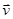в любой точке возмущенного потока определяется суммой , и определить изменение кинетической энергии, вызванное присутствием шара. Однако в большинстве случаев интерпретация этого явления связывается с изменениями, которые вызывает в жидкости движущееся тело (в данном случае шар). Рассмотрим такую постановку задачи. Пусть в начальный момент времени в выбранной системе отсчета жидкость покоится. Предположим, что в этой жидкости находится непроницаемый шар массой М, который начинает движение с нулевой начальной скоростью под действием постоянной силы. Спустя некоторое время шар будет двигаться относительно жидкости с заданной скоростью V. Предполагая, что обтекание шара в любой момент является потенциальным, применим к этой задаче полученные выше результаты.

Для определения скорости шара можно воспользоваться теоремой об изменении кинетической энергии системы шар + жидкость:

,

где А – работа приложенной силы, а – кинетическая энергия возмущения жидкости. Если в рассматриваемый момент центр движущегося шара совпадает с началом (неподвижной) системы отсчета, то распределение скоростей жидкости, обтекающей этот шар дается выражением для :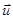

,

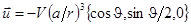а плотность кинетической энергии возмущенной жидкости -:

.

Интегрируя это выражение по всему объему, получим кинетическую энергию возмущения:

.

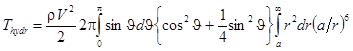Выполняя интегрирование, получим окончательно:

,

где введено обозначение .

Поскольку энергия возмущения в жидкости определяется лишь скоростью движения шара, а масса жидкости, вовлеченной в движение, не зависит от его скорости, суммарная энергия системы оказывается пропорциональной кинетической энергии движущегося шара. Учет энергии жидкости, приведенной в движение, можно произвести, добавляя к массе движущегося шара «присоединенную» массу m. Таким образом, кинетическая энергия системы шар + жидкость выражается введением присоединенной массы: 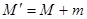. Теорема об изменении энергии системы позволяет получить эффективное динамическое уравнение движения шара в жидкости:

,

вид которого совпадает с уравнение Ньютона, но которое описывает движение системы шар + жидкость.

Дата добавления: 2015-06-28