Стационарное изэнтропийное течение газа

В рассмотренных примерах процессы сжатия сплошной среды были несущественными, что позволяло использовать модель несжимаемой идеальной жидкости. Рассмотрим теперь примеры, когда объемные деформации среды существенны. Будем называть такую сплошную среду газом. Ограничимся рассмотрением процессов, в которых вязкостью можно пренебречь. Для упрощения модели будем считать, что рассматриваемый нами газ является идеальным, т. е. уравнение состояния этого газа – уравнение Клапейрона – Менделеева, которое в переменных сплошной среды имеет вид:

,

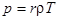где 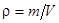- плотность газа, а .

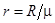Уравнение состояния дает зависимость давления от двух параметров – плотности и температуры и применимо для любых процессов. Если определить конкретный вид процесса, например изотермический или адиабатный, то одну из переменных удается исключить. Таким образом, учет термодинамических свойств системы дает необходимую информацию для полного решения задач о движении газа.

Рассмотрим в качестве примера стационарное течение газа по трубе переменного сечения, медленно изменяющегося по направлению потока.

Будем считать, что сечение трубы задано как функция координаты 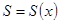, а поток газа является одномерным, т. е. его механические и термодинамические характеристики также являются функциями только одной координаты: , , , .

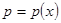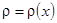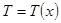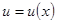Заметим, что выбранная модель не свободна от внутренних противоречий, поскольку именно составляющая скорости потока, перпендикулярная оси трубы обеспечивает выполнение условия непрерывности. По этой причине мы запишем уравнение непрерывности в интегральной форме, учитывающей этот дефект модели.

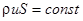
Уравнение Эйлера в проекции на направление вдоль оси трубы имеет вид

.

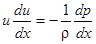В общем случае давление газа определяется его плотностью и температурой из термического уравнения состояния:

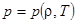
Будем считать газ идеальным, а его движение баротропным 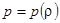. В этом случае правая часть уравнения Эйлера может быть представлена в виде

.

Производная плотности определяется из уравнения непрерывности:

,

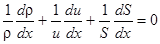так что уравнение Эйлера сводится к виду

,

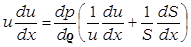что позволяет определить скорость и давление в каждом сечении трубы, если известна скорость 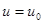в сечении .

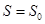Рассмотрим более подробно адиабатический процесс, считая процессы обратимыми.

В этом случае для вычисления правой части уравнения Эйлера удобно обратиться к первому началу термодинамики:

.

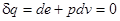Термическое уравнение (Клапейрона–Менделеева) дает соотношение 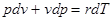, которое вместе с калорическим уравнением 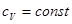определяет удельную внутреннюю энергию идеального газа 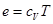и с учетом соотношения Майера 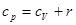позволяет представить правую часть уравнения Эйлера в виде дифференциала:

.

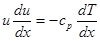Это дает интеграл уравнения Эйлера:

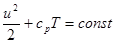. (4)

Величина 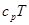является удельной энтальпией идеального газа, введенной ранее:

,

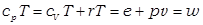так что полученный нами интеграл является интегралом Бернулли в отсутствие объемных сил:

.

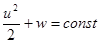Из соотношения (4) следует, что температура в адиабатическом потоке газа уменьшается с ростом его скорости. В частности, если в некотором сечении трубы 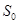, где скорость идеального газа пренебрежимо мала, температура равна 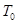, то 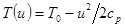. Максимально возможная скорость течения газа по трубе в этом случае определяется сечением, где температура газа равна нулю

.

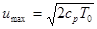Уравнение Эйлера и уравнение непрерывности позволяют определить зависимость скорости течения от площади поперечного сечения. Преобразуем правую часть уравнения Эйлера:

,

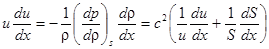где введено обозначение 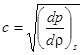. Эта величина имеет размерность скорости, и как будет показано в следующем разделе, является скоростью звука в газе в данном сечении. Отсюда получаем уравнение, связывающее скорость потока и сечение трубы:

.

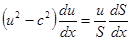Оно называется уравнением Гюгониό. Из него следует, что при 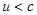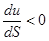, т. е. при скорости движения потока в данном сечении, меньшем скорости звука, уменьшение сечения трубы приводит к росту скорости потока. При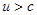 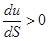т. е. при скорости движения потока, превышающей скорость звука, увеличение сечения приводит к увеличению его скорости. Если скорость течения в некотором сечении 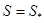равна местной скорости звука в потоке 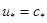, то такое сечение называется критическим.

Полученные результаты имеют большое прикладное значение для создания систем ускоряющих поток газа. При необходимости разогнать газ до большой скорости, превышающей скорость звука, сечение трубы должно вначале уменьшаться до критического, в котором скорость потока достигает местной скорости звука, а затем увеличиваться. Труба такого сечения называется соплом Лаваля и впервые была применена в паровой турбине.

Для адиабаты Пуассона 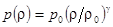скорость звука легко вычисляется:

.

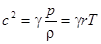Это соотношение позволяет выразить внутреннюю энергию и энтальпию идеального газа через скорость звука:

, .

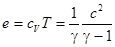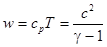Если скорость звука в покоящемся газе равна 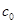(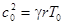), то уравнение Бернулли

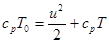
позволяет определить скорость течения газа в критическом сечении

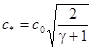
и определить зависимость температуры от скорости потока:

.

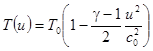Уравнение состояния и адиабата Пуассона позволяют вычислить зависимость от скорости плотности и давления идеального газа.

.

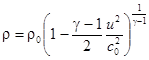
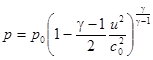Приведем также значения критических параметров потока:

, , .

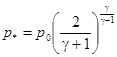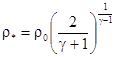Дата добавления: 2015-06-28