Разрывное течение газа в трубе постоянного сечения

В ряде случаев движение газа происходит так, что его характеристики (плотность, скорость, давление) являются разрывными функциями. Как показывает анализ, допустимо существование двух типов разрывов. Один из них не сопровождается переносом массы через поверхность разрыва. Такой разрыв называется тангенциальным. Другой тип разрыва сопровождается переносом вещества через границу разрыва. Такие разрывы называются ударными волнами, и мы рассмотрим сейчас простейшую модель этого явления.

Предположим, что движение происходит по трубе постоянного сечения вдоль оси ОХ так, что при 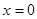имеется скачок характеристик.

Для описания разрывного течения уравнения движения в дифференциальной форме непригодны, поэтому мы будем использовать интегральные соотношения.

Закон сохранения массы в интегральной форме

применительно к рассматриваемому случаю стационарного движения по трубе постоянного сечения дает простое выражение:

.

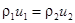Здесь индексами 1 и 2 отмечены параметры газа до и после скачка в сечении .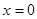

Импульс газа в выделенном контрольном объеме изменяется за счет переноса импульса через контрольную поверхность и под действием поверхностных сил:

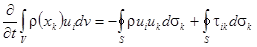
Для рассматриваемого случая эта теорема принимает вид:

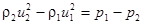
Несколько сложнее применение законов термодинамики для разрывного течения. Дело в том, что термодинамические характеристики газа введены только для равновесной системы, когда любой элементарный объем находится в состоянии термодинамического равновесия. При движении газа слева и справа от разрыва это безусловно верно. Однако, на самом скачке любой сколь угодно малый элементарный объем перестает удовлетворять нулевому началу термодинамики. Поэтому адиабатическое течение газа при прохождении через скачок параметров перестает быть изэнтропийным. Очевидно, что неравновесные процессы, которые происходят в выделенном элементарном объеме при прохождении скачка параметров, сопровождаются ростом энтропии. Следовательно, использование адиабаты Пуассона для установления соотношения между давлением и плотностью газа невозможно. Поэтому мы вернемся к основному постулату – первому началу термодинамики. Однако, применение первого начала требует некоторых дополнений. Постулаты термодинамики сформулированы для системы отсчета, в которой термодинамическая система покоится как целое. Поэтому внутренняя энергия, изменение которой рассматривается, включает лишь среднюю энергию хаотического движения

.

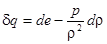В нашем случае газ движется с некоторой скоростью, поэтому мы рассмотрим изменение не внутренней энергии, а полной. На основании теоремы Кенига она равна сумме энергии движения «центра масс» и энергии движения относительно центра масс, т. е. внутренней энергии (после усреднения).

При адиабатическом процессе изменение полной энергии в выделенном объеме происходит за счет переноса энергии потоком через границу объема и за счет работы сил давления, действующих на границе. В рассматриваемом случае это дает уравнение:

.

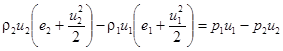Это уравнение с учетом с уравнения непрерывности приводит к уравнению Бернулли, в которое входит энтальпия системы :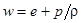

.

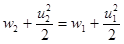Вместе с уравнениями состояния идеального газа (Клапейрона-Менделеева) 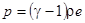и 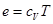система является полной системой уравнений, описывающей разрывное течение газа.

Исключая из этой системы скорости потока, можно получить соотношение, связывающее плотность и давление газа по обе стороны от разрыва:

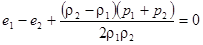
В последнем соотношении не использованы предположения о термодинамических характеристиках газа (его идеальности) и оно позволяет определить давление газа после прохождения разрыва как функцию его плотности. Такая зависимость называется ударной адиабатой или адиабатой Гюгонио. В отличие от рассматривавшейся ранее адиабаты Пуассона 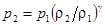, давление в ударной адиабате зависит не только от плотности газа после разрыва, но и от начальных характеристик 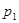и 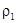. Для модели идеального газа эта зависимость имеет вид:

,

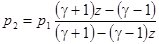где 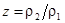– отношение плотностей газа. На рисунке изображены адиабата Пуассона и Гюгонио.

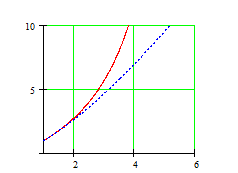
Рис.

Адиабата Пуассона (пунктир) и Гюгонио (сплошная)

При заданном начальном состоянии газа перед скачком задание лишь одного параметра после скачка, например , определяет давление газа, а следовательно, и всех остальных его параметров. Очевидно, что плотность газа не может быть сколь угодно большой. Максимальное значение плотности 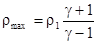. Для идеального одноатомного газа 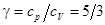, так что 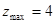, а для воздуха .

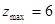Отношение температур до и после разрыва .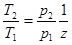

Как отмечалось выше, прохождение газом поверхности разрыва является неравновесным процессом. Установление термодинамического равновесия должно приводить к росту энтропии газа. Вычислим изменение удельной энтропии, воспользовавшись соотношением (4) для идеального газа

.

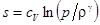Подставляя сюда значения давления, получим для изменения энтропии:

.

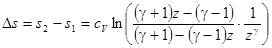Рост энтропии в системе возможен лишь при условии 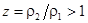, когда 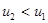, т. е. при торможении газа в ударной волне. Это условие определяет направление процессов при разрывном течении газа. Скорости потока до и после разрыва можно выразить через соответствующие скорости звука. При заданном отношении давлений они определяется выражениями:

, ,

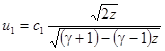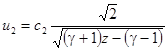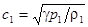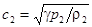где и – скорости звука в потоке слева и справа от разрыва.

Как следует из приведенных соотношений 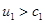, а 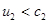, причем 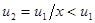. Таким образом, поток газа, втекающий в ударную волну, имеет сверхзвуковую скорость, а поток затормозившегося газа – дозвуковую.

Дата добавления: 2015-06-28