Определение. Понятие аналитической функции

Определение

Понятие аналитической функции

Пусть 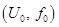— канонический элемент с центром 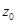. Совокупность аналитических продолжений этого элемента вдоль всевозможных путей, допускающих продолжение, называется полной аналитической функцией. Объединение кругов всех элементов называется областью существования полной аналитической функции.

Полная аналитическая функция однозначно определяется любым своим элементом.

Аналитическая функция может иметь более одного элемента с общим центром. В этом смысле аналитическая функция может оказаться многозначной.

Пусть продолжение элемента 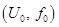возможно вдоль любого пути в области 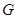с началом 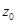. Совокупность таких продолжений называется аналитической функцией в области .

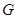Простейшим примером является совокупность элементов голоморфной в области 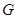функции 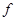. Такую аналитическую функцию отождествляют с голоморфной функцией 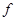и говорят, что она однозначна.

Дата добавления: 2015-06-28