Деление окружности на равные части. Построение правильных вписанных многоугольников

· Деление окружности на четыре части (рис. 2.20). Два взаимноперпендикулярных диаметра делят окружность на четыре равные части. Соединяя точки деления, получают вписанный квадрат.

· Деление окружности на восемь равных частей (рис. 2.21). Дуги между точками А и С, В и С делят пополам при помощи циркуля. Точки деления соединяют с центром окружности и продолжают до пересечения с противоположной половиной окружности. Соединяя точки деления, получают правильный вписанный восьмиугольник.

Рис. 2.20

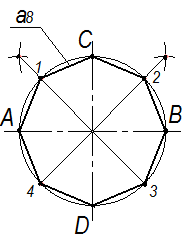Рис. 2.21

· Деление окружности на три равные части (рис. 2.22). Из точки D конца вертикального диаметра как из центра радиусом окружности проводят дугу, пересекающую окружность в точках М и N. Соединив точки М, N и С, получают правильный вписанный треугольник.

Рис. 2.22

Рис. 2.23

· Деление окружности на шесть равных частей (рис. 2.23). Из концов А и В горизонтального диаметра радиусом окружности проводят дуги, пересекающие окружность в точках 1, 2, 3, и 4. Соединив точки деления между собой и с А и В, получают правильный вписанный шестиугольник. На рис. 24 показано построение правильного двенадцатиугольника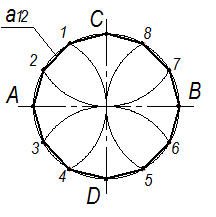

Рис. 2.24

Рис. 2.25

· Деление окружности на семь равных частей (рис. 2.25). Разделив окружность на три равные части, получают хорду MN – сторону правильного вписанного треугольника. Половина этой хорды с достаточным приближением равна стороне вписанного семиугольника.

· Деление окружности на пять и десять равных частей (рис. 2.26). Радиус окружности ОВ делят на две равные части и, принимая точку 0₁ за центр, проводят дугу радиусом, равным отрезку 0₁С. Эта дуга пересекает горизонтальный диаметр окружности в точке Е. Отрезок ЕС дает величину стороны правильного вписанного пятиугольника, а отрезок Е0 приближенно равен стороне вписанного десятиугольника.

Рис. 2.26

· Деление окружности на равные части при помощи таблицы хорд. Например, в окружность диаметром 80 мм вписать правильный девятиугольник. По таблице определяют коэффициент – 0,342. Длина хорды – 80 × 0,342 = 27,36 мм. На окружности диаметром 80 мм откладывают девять раз найденное значение длины хорды. Соединив точки деления, получают правильный девятиугольник.

Деление окружности на равные части (таблица хорд).

Кол-во частей	Длина хорды на единицу длины диаметра		Число сторон правильного многоугольника	Диаметр описанной окружности d
	0,866			1,154 а
				1,414 а
	0,588			1,702 а
	0,500			2,000 а
	0,434			2,304 а
	0,383			2,614 а
	0,342			2,924 а
	0,309			3,230 а
	0,282			3,550 а
	0,258			3,864 а
	0,239
	0,223

Деление окружности на равные части при помощи угольника и линейки приведены на рис. 2.27.

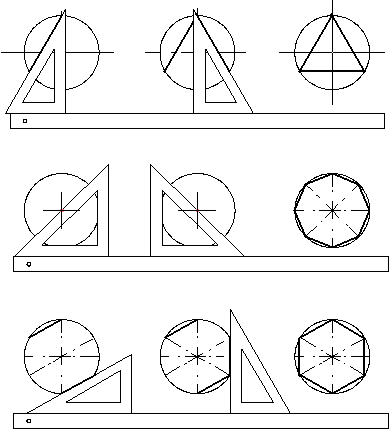
Рис. 2.27

Дата добавления: 2015-06-28