Растяжение и сжатие

Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая или сжимающая), а все остальные внутренние силовые факторы равны нулю.

Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными.

Продольные силы определяются с помощью метода сечений.

Пример 1: Пусть имеется ступенчатый стержень, нагруженный силами Р ₁ = 2 кН, Р ₂ = 3 кН и Р ₃ = 2 кН вдоль оси стержня, показанного на рис. 1.14, а. Определить величину продольных сил.

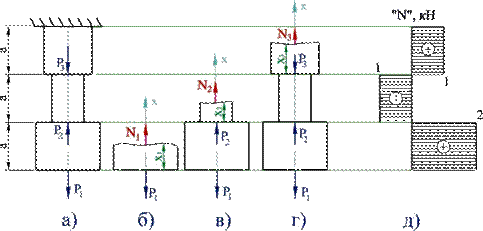
Рисунок 1.14

Решение. Стержень делим на участки по местам приложения нагрузок и по местам изменения поперечного сечения.

Первый участок ограничен точками приложения сил Р ₁ и Р ₂. Направим ось 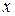вдоль оси участка вверх с началом координат в точке приложения силы Р ₁ (начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии х ₁ от начала первого участка. Причем координата х ₁ может быть взята в интервале 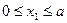, где а - длина первого участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой N ₁, предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

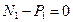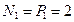; , кН

Положительный знак продольной силы говорит о том, что первый участок растянут.

Значение продольной силы не зависит от координаты х ₁, поэтому на всем участке значение продольной силы постоянно и равно N ₁.

Второй участок ограничен точками приложения сил Р ₂ и Р ₃. Направим ось х вдоль оси участка вверх с началом координат в точке приложения силы Р ₂ (начало второго участка).

Мысленно рассечем второй участок поперечным сечением на расстоянии х ₂ от начала второго участка. Причем координата х ₂ может быть взята в интервале 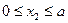, где а - длина второго участка.

Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой N ₂, предварительно направив ее в сторону растяжения рассматриваемой части.

Из условия равновесия статики:

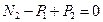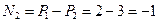; , кН

Знак минус говорит о том, что второй участок сжат.

Аналогично для третьего участка:

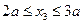
; , кН

Полученные результаты для большей наглядности удобней представить в виде графика (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.14, д). В одну сторону откладываем положительные значения, в другую - отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («N») и через запятую - единицы измерения (кН)

Пример 2: Два стержня, соединенные в т. А, находятся под действием силы Р (рис. 1.15, а). Определить усилия, действующие в стержнях.

	а)		б)		в)

Решение.

Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n - n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N ₁ и N ₂ в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис. 1.15, б).

Уравновесим отсеченную часть, запишем уравнения: .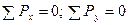

Решая, из первого уравнения получим:

,

из второго уравнения окончательно имеем:

; .

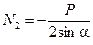Так как величина силы N ₂ < 0, то её направление следует изменить на противоположное (рис. 1.15, в). Согласно рисунку нормальная сила N ₁ растягивает отсеченную часть стержня 1 - она положительна, сила N ₂ сжимает отсеченную часть стержня 2 - она отрицательна.

Пример 3: Абсолютно жесткий брус подвешен на двух стержнях и находится под действием силы Р (рис. 1.16,а). Определить усилия в стержнях.

Используя метод сечений, получим отсеченную часть, показанную на рис. 1.16,б.

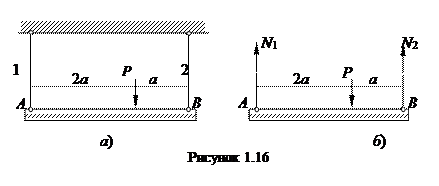
Запишем уравнения равновесия: 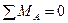и :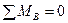

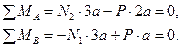
Решая систему уравнений, получим:

; .

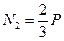Дата добавления: 2015-06-28