Диаграмма растяжения стали марки Ст3

Рассмотрим характерные участки и точки диаграммы растяжения малоуглеродистой стали, а также соответствующие им стадии деформирования образца (рис. 2.2).

От начала нагружения до определенного значения растягивающей силы имеет место прямая пропорциональная зависимость между силой и удлинением образца. Эта зависимость выражается на диаграмме прямой ОА. На этой стадии растяжения справедлив закон Гука. Обозначим силу, при которой закон пропорциональности прекращает свое действие, через Р _пц. Этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой Р _пц, называется пределом пропорциональности и вычисляется по формуле: s_пц = Р _пц/ F ₀.

Пределом пропорциональности s_пц называется напряжение, после которого нарушается закон Гука. Для Ст3 s_пц» 200 МПа.

Деформация называется упругой, если она полностью исчезает после разгрузки. Постепенно повышая нагрузку, будем проводить полную разгрузку образца. Пока сила Р не достигнет определенной величины, вызванные ею деформации будут исчезать при разгрузке. Процесс разгружения при этом изобразится той же линией, что и нагружение. Обозначим через Р _у наибольшее значение силы, при котором образец еще не дает при разгрузке остаточной деформации. Этому значению на диаграмме соответствует точка В, а упругой стадии растяжения образца - участок ОВ.

Наибольшее напряжение, до которого остаточная деформация образца не обнаруживается при разгрузке, называется пределом упругости s_у = Р _у / F ₀. Обычно за предел упругости принимают напряжение, при котором остаточная деформация достигает 0,001¸0,005 %. При этом предел упругости обозначается через s_0,001 или s_0,005. Для Ст3 s_у» 210 МПа.

Далее кривая плавно поднимается до точки C, где наблюдается переход к горизонтальному участку CD, называемому площадкой текучести. На этой стадии удлинение образца растет при постоянном значении растягивающей силы, обозначаемой Р _т. Такой процесс деформации называется текучестью материала.

Пределом текучести называется наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающем усилии, s_т = Р _т / F ₀. Для Ст3 s_т = 240 МПа.

После стадии текучести материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации. Этому процессу соответствует восходящий участок DE диаграммы, называемый участком упрочнения. Точка E соответствует наибольшему усилию Р _max, которое может воспринять образец.

Напряжение, соответствующее максимальной силе Р _max, называется временным сопротивлением или пределом прочности s_в = Р _max / F ₀. Для Ст3 s_В» 400 МПа.

После достижения усилия Р _max деформация происходит на небольшой длине образца. Это ведет к образованию местного сужения в виде шейки и к падению силы Р, не смотря на то, что напряжение в сечении шейки непрерывно растет.

Обозначив через Р _к величину растягивающей силы в момент разрыва, получим:

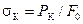. (2.1)

Если в процессе растяжения дойти до некоторой точки М, напряжение для которой выше предела упругости, а затем начать разгрузку, то линия разгрузки будет выражаться прямой MN, параллельной начальному участку диаграммы OB. При полном снятии нагрузки в образце сохраняется остаточная деформация D l _ост. Полная деформация испытываемого образца состоит из двух частей:

,

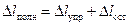где D l _упр - упругая деформация, исчезающая после снятия нагрузки; D l _ост - остаточная деформация.

После испытания образца определяют относительное остаточное удлинение при разрыве:

,

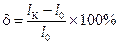и относительное остаточное сужение в шейке:

,

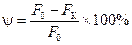где l _К и F _К - длина образца и площадь поперечного сечения в шейке после разрыва. Величины d и y являются характеристиками пластичности материала. Для Ст3 d = 21¸27 %; y = 60¸70 %.

Разделив нагрузку P на начальную площадь поперечного сечения F ₀, а абсолютное удлинение D l на расчетную длину образца l ₀, получим так называемую диаграмму напряжений в координатах s-e (рис. 2.3), вид которой совпадает с диаграммой растяжения. Из диаграммы видно, что:

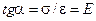, (Закон Гука)

где Е - модуль продольной упругости (модуль упругости первого рода, модуль Юнга).

Если в ходе испытания измерять поперечную деформацию e¢ и следить за изменением отношения e¢/e, то можно обнаружить, что в зоне малых упругих деформаций это отношение останется практически постоянным. Величину 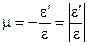называют коэффициентом поперечной деформации или коэффициентом Пуассона. Величины Е и m характеризуют упругие свойства материалов, поэтому их называют упругими постоянными. Для Ст3 Е = 2×10⁵ МПа; m = 0,3.

Нисходящий участок ЕК диаграммы напряжений носит условный характер, поскольку площадь поперечного сечения образца непрерывно уменьшается после образования шейки. Деля величину силы на действительную площадь поперечного сечения образца F_i, можно построить истинную диаграмму напряжений. Истинное сопротивление в момент разрыва определяется .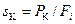

Дата добавления: 2015-06-28