Деформации при растяжении (сжатии)

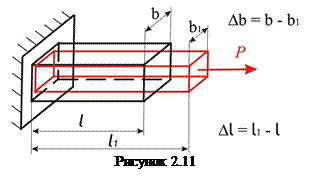При растяжении стержня постоянного поперечного сечения длина увеличивается, а поперечные размеры уменьшаются (рис. 2.11).

Из закона Гука:

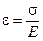. (2.4)

Учитывая то, что e = D l / l и s = N / F имеем:

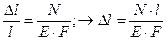. (2.5)

Знаменатель E × F называют жесткостью при растяжении - сжатии или продольной жесткостью.

Если мы возьмем произвольный поперечный размер b, то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 2.8):

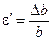. (2.6)

Между поперечной и продольной относительной деформацией при простом растяжении (сжатии) в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название коэффициента Пуассона и обозначается буквой m:

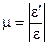. (2.7)

Учитывая, что продольная и поперечная деформация всегда имеют противоположные знаки, получаем:

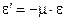. (2.8)

Коэффициент Пуассона наряду с модулем продольной упругости характеризует упругие свойства материалов.

Значения m для различных материалов определяются экспериментально и изменяются в пределах 0 £ m £ 0,5 (m = 0 у пробки; m = 0,5 у резины; m = 0,3 у стали).

В некоторых случаях для обеспечения нормальной работы конструкций размеры их элементов нужно выбирать так, чтобы обеспечивалось условие жесткости. При растяжении (сжатии) условие жесткости имеет следующий вид:

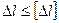, (2.9)

где D l - изменение размеров детали; [D l ] - допускаемая величина этого изменения.

Расчет по условию жесткости всегда следует дополнять расчетом на прочность.

На растяжение работает и круглая труба, нагруженная внутренним давлением (рис. 2.12, а). Для определения напряжения в стенке такой трубы найдем из рассмотрения равновесия половины трубы (рис. 2.12, б) силу N, разрывающую стенку:

,

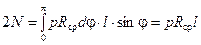откуда

,

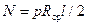где р - давление в трубе; R _ср – средний радиус трубы; l - длина трубы.

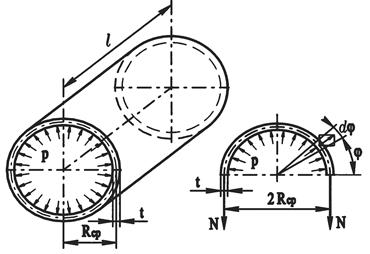
а) б)

Рисунок 2.12

Условие прочности трубы получаем в виде:

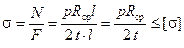. (2.10)

где t - толщина стенки трубы.

Деформацию трубы - увеличение ее диаметра D - найдем из закона Гука 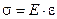: так как напряжение 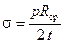, а относительная деформация 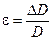, то

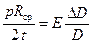
откуда

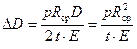. (2.11)

Дата добавления: 2015-06-28