Статические моменты сечений

Статическим моментом S _x сечения относительно оси х называется геометрическая характеристика, определяемая интегралом вида:

, (3.1)

где у - расстояние от элементарной площадки dF до оси х.

Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (3.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механики теореме Вариньона о моменте равнодействующей можно написать:

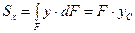_, (3.2)

где F - площадь сечения представляет собой равнодействующую; у_с - координата плечо равнодействующей; С - центр тяжести сечения.

Аналогично, статический момент относительно оси у равен:

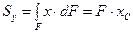, (3.3)

откуда следуют формулы для определения координат центра тяжести:

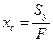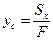_{, .} (3.4)

Статические моменты могут быть положительными, отрицательными и равными нулю. В частности, относительно любых центральных осей (проходящих через центр тяжести С обозначаются х_с, у_с) статические моменты 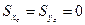. Размерность статических моментов L ³. Для сложного сечения, состоящего из n частей, выражения (3.2), (3.3) можно представить в виде:

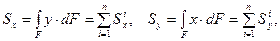(3.5)

где 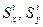- статические моменты i -й части сечения относительно осей х и у соответственно.

Таким образом, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей сечения относительно той же оси.

Для определения статических моментов сложной фигуры ее разбивают на простые части, для каждой из которых известна площадь F_i и положение центра тяжести x_i и y_i (рис. 3.2).

Рисунок 3.2

Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:

; .

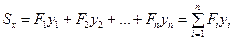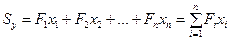Отсюда координаты центра тяжести сложной фигуры:

;

.

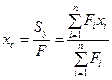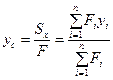Пример 1: Определить координаты центра тяжести фигуры (рис. 3.3).

Рисунок 3.3

Разбиваем фигуру на два прямоугольника:

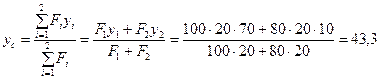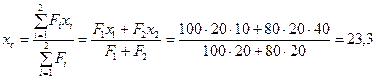ед.;

ед.

Дата добавления: 2015-06-28